12. 已知等腰三角形的周长为 12,设腰长为$x$,底边长为$y$.
(1)试写出$y$关于$x$的函数表达式,并直接写出自变量$x$的取值范围;
(2)当$x=5$时,求出函数值.
(1)试写出$y$关于$x$的函数表达式,并直接写出自变量$x$的取值范围;
(2)当$x=5$时,求出函数值.
答案:解:(1)由题意得 $ 12 = 2x + y $,$ \therefore y = 12 - 2x $,
根据题意可得 $ y < 2x $,$ 2x < 12 $,$ \therefore 3 < x < 6 $。
(2)由(1)得 $ y = 12 - 2x $,
$ \therefore $当 $ x = 5 $ 时,$ y = 12 - 2 \times 5 = 2 $,即函数值为 2。
根据题意可得 $ y < 2x $,$ 2x < 12 $,$ \therefore 3 < x < 6 $。
(2)由(1)得 $ y = 12 - 2x $,
$ \therefore $当 $ x = 5 $ 时,$ y = 12 - 2 \times 5 = 2 $,即函数值为 2。
13. (2023·连云港)目前,我市对市区居民用气户的燃气收费,以户为基础、年为计算周期设定了如下表的三个气量阶梯:
|阶梯|年用气量|销售价格|备注|
|----|----|----|----|
|第一阶梯|$0\sim 400m^{3}$(含 400)的部分|$2.67元/m^{3}$|若家庭人口超过 4 人的,每增加 1 人,第一、二阶梯年用气量的上限分别增加$100m^{3}$、$200m^{3}$|
|第二阶梯|$400\sim 1200m^{3}$(含 1200)的部分|$3.15元/m^{3}$| |
|第三阶梯|$1200m^{3}$以上的部分|$3.63元/m^{3}$| |
(1)一户家庭人口为 3 人,年用气量为$200m^{3}$,则该年此户需缴纳燃气费用为
(2)一户家庭人口不超过 4 人,年用气量为$xm^{3}(x>1200)$,该年此户需缴纳燃气费用为$y$元,求$y$与$x$的函数表达式;
(3)甲户家庭人口为 3 人,乙户家庭人口为 5 人,某年甲户、乙户缴纳的燃气费用均为 3855 元,该年乙户比甲户多用多少立方米的燃气? (结果精确到$1m^{3}$)
|阶梯|年用气量|销售价格|备注|
|----|----|----|----|
|第一阶梯|$0\sim 400m^{3}$(含 400)的部分|$2.67元/m^{3}$|若家庭人口超过 4 人的,每增加 1 人,第一、二阶梯年用气量的上限分别增加$100m^{3}$、$200m^{3}$|
|第二阶梯|$400\sim 1200m^{3}$(含 1200)的部分|$3.15元/m^{3}$| |
|第三阶梯|$1200m^{3}$以上的部分|$3.63元/m^{3}$| |
(1)一户家庭人口为 3 人,年用气量为$200m^{3}$,则该年此户需缴纳燃气费用为
534
元;(2)一户家庭人口不超过 4 人,年用气量为$xm^{3}(x>1200)$,该年此户需缴纳燃气费用为$y$元,求$y$与$x$的函数表达式;
(3)甲户家庭人口为 3 人,乙户家庭人口为 5 人,某年甲户、乙户缴纳的燃气费用均为 3855 元,该年乙户比甲户多用多少立方米的燃气? (结果精确到$1m^{3}$)
答案:(1)534
(2)解:根据题意,得 $ y = 400 \times 2.67 + (1200 - 400) \times 3.15 + 3.63(x - 1200) = 3.63x - 768 $,
$ \therefore y $ 与 $ x $ 的函数表达式为 $ y = 3.63x - 768(x > 1200) $。
(3)解:$ \because 400 \times 2.67 + (1200 - 400) \times 3.15 = 3588 < 3855 $,$ \therefore $甲户该年的用气量达到了第三阶梯。
当 $ y = 3855 $ 时,$ 3.63x - 768 = 3855 $,解得 $ x \approx 1273.6 $。
$ 400 + 100 = 500(m^{3}) $,$ 1200 + 200 = 1400(m^{3}) $。
又 $ \because 2.67 \times 500 = 1335 < 3855 $,且 $ 2.67 \times 500 + 3.15 \times (1400 - 500) = 4170 > 3855 $,$ \therefore $乙户该年的用气量达到第二阶梯,但未达到第三阶梯。设乙户该年的用气量为 $ a m^{3} $,则有 $ 2.67 \times 500 + 3.15(a - 500) = 3855 $,解得 $ a = 1300 $。
$ 1300 - 1273.6 \approx 26(m^{3}) $。
答:该年乙户比甲户多用约 $ 26 m^{3} $ 的燃气。
(2)解:根据题意,得 $ y = 400 \times 2.67 + (1200 - 400) \times 3.15 + 3.63(x - 1200) = 3.63x - 768 $,
$ \therefore y $ 与 $ x $ 的函数表达式为 $ y = 3.63x - 768(x > 1200) $。
(3)解:$ \because 400 \times 2.67 + (1200 - 400) \times 3.15 = 3588 < 3855 $,$ \therefore $甲户该年的用气量达到了第三阶梯。
当 $ y = 3855 $ 时,$ 3.63x - 768 = 3855 $,解得 $ x \approx 1273.6 $。
$ 400 + 100 = 500(m^{3}) $,$ 1200 + 200 = 1400(m^{3}) $。
又 $ \because 2.67 \times 500 = 1335 < 3855 $,且 $ 2.67 \times 500 + 3.15 \times (1400 - 500) = 4170 > 3855 $,$ \therefore $乙户该年的用气量达到第二阶梯,但未达到第三阶梯。设乙户该年的用气量为 $ a m^{3} $,则有 $ 2.67 \times 500 + 3.15(a - 500) = 3855 $,解得 $ a = 1300 $。
$ 1300 - 1273.6 \approx 26(m^{3}) $。
答:该年乙户比甲户多用约 $ 26 m^{3} $ 的燃气。
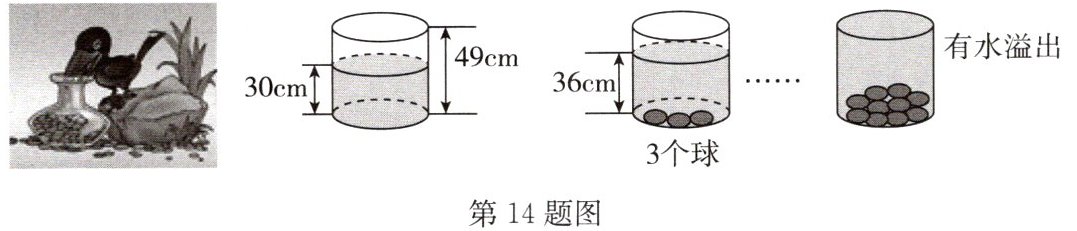
14. 小青同学受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球,量筒中水面升高
(2)直接写出放入小球后量筒中水面的高度$y(cm)$与放入小球的个数$x$之间的函数表达式(不需要写出自变量的取值范围),并求出当$x=6$时$y$的值;
(3)量筒中至少放入几个小球时有水溢出?
(1)放入一个小球,量筒中水面升高
2
cm;(2)直接写出放入小球后量筒中水面的高度$y(cm)$与放入小球的个数$x$之间的函数表达式(不需要写出自变量的取值范围),并求出当$x=6$时$y$的值;
(3)量筒中至少放入几个小球时有水溢出?

答案:(1)2
(2)解:由题意可得,$ y = 30 + 2x $,
当 $ x = 6 $ 时,$ y = 30 + 2 \times 6 = 42 $,
即放入小球后量筒中水面的高度 $ y(cm) $ 与放入小球的个数 $ x $ 之间的函数关系式是 $ y = 2x + 30 $,当 $ x = 6 $ 时,$ y $ 的值是 42。
(3)解:由题意,得 $ 2x + 30 > 49 $,解得 $ x > 9.5 $。
答:量筒中至少放入 10 个小球时有水溢出。
(2)解:由题意可得,$ y = 30 + 2x $,
当 $ x = 6 $ 时,$ y = 30 + 2 \times 6 = 42 $,
即放入小球后量筒中水面的高度 $ y(cm) $ 与放入小球的个数 $ x $ 之间的函数关系式是 $ y = 2x + 30 $,当 $ x = 6 $ 时,$ y $ 的值是 42。
(3)解:由题意,得 $ 2x + 30 > 49 $,解得 $ x > 9.5 $。
答:量筒中至少放入 10 个小球时有水溢出。