1.(2023·通辽)在平面直角坐标系中,一次函数$y = 2x - 3$的图象是 (

D
)
答案:D
2.直线$y = 2x - 3$与$x$轴、$y$轴的交点坐标分别是 (
A.$(\frac {3}{2},0),(0,-3)$
B.$(-\frac {3}{2},0),(0,-3)$
C.$(\frac {3}{2},0),(0,3)$
D.$(-\frac {3}{2},0),(0,3)$
A
)A.$(\frac {3}{2},0),(0,-3)$
B.$(-\frac {3}{2},0),(0,-3)$
C.$(\frac {3}{2},0),(0,3)$
D.$(-\frac {3}{2},0),(0,3)$
答案:A
3.(泰州中考)点$P(a,b)$在函数$y = 3x + 2$的图象上,则代数式$6a - 2b + 1$的值等于 (
A.5
B.3
C.-3
D.-1
C
)A.5
B.3
C.-3
D.-1
答案:C
4.(2024·通辽)如图,在同一平面直角坐标系中,一次函数$y = k_{1}x + b_{1}$与$y = k_{2}x + b_{2}$(其中$k_{1}k_{2}≠0,k_{1},k_{2},b_{1},b_{2}$为常数)的图象分别为直线$l_{1},l_{2}$.下列结论正确的是 (

A.$b_{1} + b_{2}>0$ B.$b_{1}b_{2}>0$ C.$k_{1} + k_{2}<0$ D.$k_{1}k_{2}<0$
A.$b_{1} + b_{2}>0$
B.$b_{1}b_{2}>0$
C.$k_{1} + k_{2}<0$
D.$k_{1}k_{2}<0$
A
)
A.$b_{1} + b_{2}>0$ B.$b_{1}b_{2}>0$ C.$k_{1} + k_{2}<0$ D.$k_{1}k_{2}<0$
A.$b_{1} + b_{2}>0$
B.$b_{1}b_{2}>0$
C.$k_{1} + k_{2}<0$
D.$k_{1}k_{2}<0$
答案:A
5.一次函数$y = -\frac {1}{2}x + 1$的图象如图所示,当$-1≤y<3$时,$x$的取值范围是

$-4 < x \leq 4$
.
答案:$-4 < x \leq 4$
6.直线$y = mx + n$如图所示,化简:$|m - n| - \sqrt {m^{2}}=$

$n$
.
答案:$n$
7.一次函数$y = 6 - x$与正比例函数$y = kx$的图象如图所示,则$k$的值为

2
.
答案:2
8.已知一次函数的图象经过点$(-4,-9),(3,5)$和$(a,6)$,求$a$的值.
答案:解:设一次函数表达式为 $y = kx + b(k \neq 0)$,
依题意,得 $\begin{cases}3k + b = 5, \\ -4k + b = -9,\end{cases}$ 解得 $\begin{cases}k = 2, \\ b = -1,\end{cases}$
$\therefore$ 一次函数表达式为 $y = 2x - 1$。
将 $(a,6)$ 代入 $y = 2x - 1$ 中,得 $2a - 1 = 6$,解得 $a = \frac{7}{2}$。
依题意,得 $\begin{cases}3k + b = 5, \\ -4k + b = -9,\end{cases}$ 解得 $\begin{cases}k = 2, \\ b = -1,\end{cases}$
$\therefore$ 一次函数表达式为 $y = 2x - 1$。
将 $(a,6)$ 代入 $y = 2x - 1$ 中,得 $2a - 1 = 6$,解得 $a = \frac{7}{2}$。
9.在如图所示的直角坐标系中分别作出$y = -2x$与$y = -2x + 3$的图象,并说出两个图象之间的关系,以及各自函数图象的特点.


答案:
解:根据题意,作出图象,如答图。
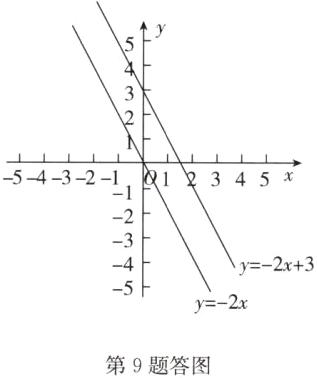
观察可得,在同一坐标系中,两个函数图象平行,且 $y = -2x$ 的图象在 $y = -2x + 3$ 的图象的下方,
函数 $y = -2x$ 的图象经过第二、四象限,$y$ 随 $x$ 的增大而减小;
函数 $y = -2x + 3$ 的图象经过第一、二、四象限,$y$ 随 $x$ 的增大而减小。
解:根据题意,作出图象,如答图。

观察可得,在同一坐标系中,两个函数图象平行,且 $y = -2x$ 的图象在 $y = -2x + 3$ 的图象的下方,
函数 $y = -2x$ 的图象经过第二、四象限,$y$ 随 $x$ 的增大而减小;
函数 $y = -2x + 3$ 的图象经过第一、二、四象限,$y$ 随 $x$ 的增大而减小。