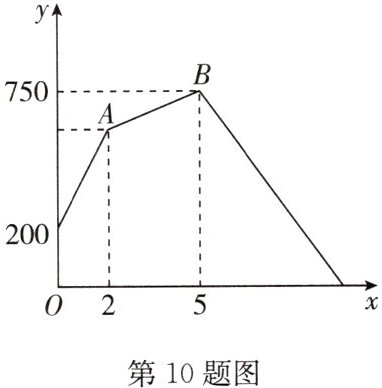
10.(2024·玄武区模拟)某小区的快递驿站有揽收员甲负责扫描快递入库,派送员乙负责运送快递出库.仓库里原有快递 200 件,已知甲平均每小时扫描 200 件快递入库,甲工作 2 小时后,乙开始工作.又过了 3 小时,甲因故离开,乙按原速工作.仓库里的快递数量 y(件)与时间 x(时)之间的关系如图.
(1)点 A 的坐标为
(2)分别求出 $2 \leq x \leq 5$ 和 $x \geq 5$ 时,y 与 x 之间的函数表达式;
(3)若仓库里的快递数量不少于 a 件称作仓库“半饱和”,已知“半饱和”状态持续了 $\frac{8}{3}$ 小时,求 a 的值.
(1)点 A 的坐标为
(2,600)
,派送员乙平均每小时的送件量为150
件;(2)分别求出 $2 \leq x \leq 5$ 和 $x \geq 5$ 时,y 与 x 之间的函数表达式;
(3)若仓库里的快递数量不少于 a 件称作仓库“半饱和”,已知“半饱和”状态持续了 $\frac{8}{3}$ 小时,求 a 的值.

答案:(1) $(2,600)$ 150
(2) 解: 当 $2 \leq x \leq 5$ 时,设 y 与 x 之间的函数表达式为 $y = k_1x + b_1(k_1,b_1$ 为常数,且 $k_1 \neq 0)$。将 $(2,600)$ 和 $(5,750)$ 代入 $y = k_1x + b_1$,
得 $\begin{cases}2k_1 + b_1 = 600,\\5k_1 + b_1 = 750,\end{cases}$ 解得 $\begin{cases}k_1 = 50,\\b_1 = 500,\end{cases}$
$\therefore y = 50x + 500(2 \leq x \leq 5)$。
派送员乙送 750 件快递需要的时间是 $750 \div 150 = 5$(时),
$\therefore$ 函数图象与 x 轴的交点坐标是 $(10,0)$。
当 $x \geq 5$ 时,设 y 与 x 之间的函数表达式为 $y = k_2x + b_2(k_2,b_2$ 为常数,且 $k_2 \neq 0)$。将 $(5,750)$ 和 $(10,0)$ 代入 $y = k_2x + b_2$,得 $\begin{cases}5k_2 + b_2 = 750,\\10k_2 + b_2 = 0,\end{cases}$ 解得 $\begin{cases}k_2 = -150,\\b_2 = 1500,\end{cases}$
$\therefore y$ 与 x 之间的函数表达式为 $y = -150x + 1500(5 \leq x \leq 10)$。
(3) 解: $\because \frac{8}{3} < 3$,$\therefore a > 600$。
当 $2 \leq x \leq 5$ 时,$50x + 500 = a$,解得 $x = \frac{a - 500}{50}$;
当 $x \geq 5$ 时,$-150x + 1500 = a$,解得 $x = \frac{1500 - a}{150}$。
由题意得 $\frac{1500 - a}{150} - \frac{a - 500}{50} = \frac{8}{3}$,解得 $a = 650$。
(2) 解: 当 $2 \leq x \leq 5$ 时,设 y 与 x 之间的函数表达式为 $y = k_1x + b_1(k_1,b_1$ 为常数,且 $k_1 \neq 0)$。将 $(2,600)$ 和 $(5,750)$ 代入 $y = k_1x + b_1$,
得 $\begin{cases}2k_1 + b_1 = 600,\\5k_1 + b_1 = 750,\end{cases}$ 解得 $\begin{cases}k_1 = 50,\\b_1 = 500,\end{cases}$
$\therefore y = 50x + 500(2 \leq x \leq 5)$。
派送员乙送 750 件快递需要的时间是 $750 \div 150 = 5$(时),
$\therefore$ 函数图象与 x 轴的交点坐标是 $(10,0)$。
当 $x \geq 5$ 时,设 y 与 x 之间的函数表达式为 $y = k_2x + b_2(k_2,b_2$ 为常数,且 $k_2 \neq 0)$。将 $(5,750)$ 和 $(10,0)$ 代入 $y = k_2x + b_2$,得 $\begin{cases}5k_2 + b_2 = 750,\\10k_2 + b_2 = 0,\end{cases}$ 解得 $\begin{cases}k_2 = -150,\\b_2 = 1500,\end{cases}$
$\therefore y$ 与 x 之间的函数表达式为 $y = -150x + 1500(5 \leq x \leq 10)$。
(3) 解: $\because \frac{8}{3} < 3$,$\therefore a > 600$。
当 $2 \leq x \leq 5$ 时,$50x + 500 = a$,解得 $x = \frac{a - 500}{50}$;
当 $x \geq 5$ 时,$-150x + 1500 = a$,解得 $x = \frac{1500 - a}{150}$。
由题意得 $\frac{1500 - a}{150} - \frac{a - 500}{50} = \frac{8}{3}$,解得 $a = 650$。