1. 有一张三角形纸片ABC,已知$∠B=∠C=α$,按下列方案用剪刀沿着箭头方向剪开,所剪下的三角形纸片不一定是全等图形的是 (
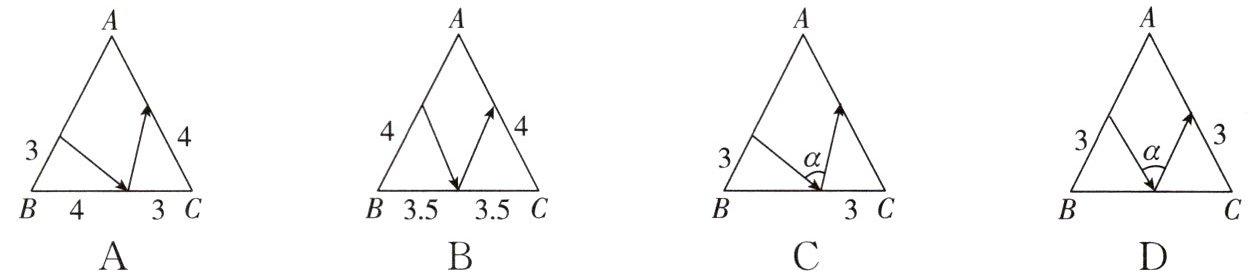
D
)
答案:D
2. 如图,已知$∠1=∠2$,要说明$△ABD\cong △ACD$,还需从条件①$∠ADB=∠ADC$,②$∠B=∠C$,③$DB=DC$,④$AB=AC$中选一个,则正确的选法有 (

A. 1种
B. 2种
C. 3种
D. 4种
C
)
A. 1种
B. 2种
C. 3种
D. 4种
答案:C
3. (2024·启东期末)如图,在方格纸中,以AB为一边作$△ABP$,使之与$△ABC$全等,从$P_{1},P_{2},P_{3},P_{4}$四个点中找出符合条件的点P,则点P有 (

A. 1个
B. 2个
C. 3个
D. 4个
C
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:C
4. 如图,已知$AB⊥CD,AB=CD$,E,F是AD上的两个点,$CE⊥AD,BF⊥AD$,若$AD=a,BF=b,CE=c$,则EF的长为 (

A. $a+b-c$
B. $b+c-a$
C. $a+c-b$
D. $a-b$
B
)
A. $a+b-c$
B. $b+c-a$
C. $a+c-b$
D. $a-b$
答案:B
5. 在学习了全等三角形的判定后,小龙编了这样一个题目:如图,已知$AB=CD,∠A=∠D,AO=DO$,求证:$△ABO\cong △DCO$.老师说他的已知条件给多了,你帮他去掉一个已知条件:________________________.(写出一个即可)


$AO=DO$(或$AB=CD$)
答案:$ AO = DO $(或$ AB = CD $)
6. (2024·扬中期末)如图,在$△ABC$中,$∠B=∠C=65^{\circ }$,点D,E,F分别在边BC,AB,AC上,如果$BD=CF,BE=CD$,那么$∠EDF=$

65
度.
答案:65
7. (2023春·丹阳期中)如图,在四边形ABCD中,$∠ADC=∠ABC=90^{\circ },AD=CD,DP⊥AB$于点P.若四边形ABCD的面积是9,则DP的长是______

3
.
答案:3