1. 已知一次函数 $ y = kx - 1(k \neq 0) $,若 $ y $ 随 $ x $ 的增大而减小,则它的图象不经过(
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
A
)A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:A
2. 数形结合是解决数学问题常用的思想方法. 如图,直线 $ y = x + 5 $ 和直线 $ y = ax + b $ 相交于点 $ P $,根据图象可知,关于 $ x $ 的方程 $ x + 5 = ax + b $ 的解是(
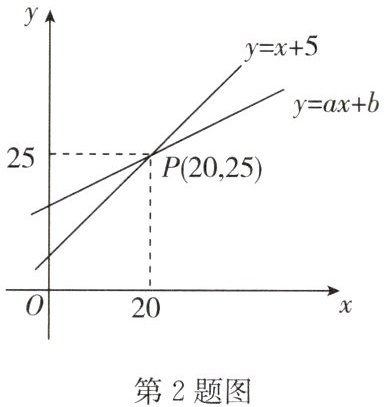
A. $ x = 20 $
B. $ x = 5 $
C. $ x = 25 $
D. $ x = 15 $
A
)
A. $ x = 20 $
B. $ x = 5 $
C. $ x = 25 $
D. $ x = 15 $
答案:A
3. 若点 $ A(m,n) $ 在一次函数 $ y = 3x + b $ 的图象上,且 $ 3m - n > 2 $,则 $ b $ 的取值范围为(
A. $ b < - 2 $
B. $ b > - 2 $
C. $ b < 2 $
D. $ b > 2 $
A
)A. $ b < - 2 $
B. $ b > - 2 $
C. $ b < 2 $
D. $ b > 2 $
答案:A
4. 如图是小明的身高随年龄变化的部分图象,那么小明自 16 岁到 18 岁这两年间身高一共增高了约

12
cm.(结果保留整数)
答案:12
5. 把直线 $ y = 2x - 1 $ 向左平移 1 个单位长度,再向上平移 2 个单位长度,则平移后所得直线的函数表达式为
y = 2x + 3
.答案:y = 2x + 3
6. 设一次函数 $ y = k_1x + b_1(k_1 \neq 0) $ 的图象为直线 $ l_1 $,一次函数 $ y = k_2x + b_2(k_2 \neq 0) $ 的图象为直线 $ l_2 $,若 $ k_1 = k_2 $,且 $ b_1 \neq b_2 $,我们就称直线 $ l_1 $ 与直线 $ l_2 $ 互相平行. 如图,求过点 $ P(1,4) $ 且与已知直线 $ y = - 2x - 1 $ 平行的直线 $ l $ 的函数表达式,并在图中画出直线 $ l $.


答案:
解:∵直线 l 与直线 y = -2x - 1 平行,
∴设直线 l 的函数表达式为 y = -2x + b,
∵直线 l 过点 P(1,4),∴ 4 = -2×1 + b,解得 b = 6,
∴直线 l 的函数表达式为 y = -2x + 6。
画出直线 l,如答图。

解:∵直线 l 与直线 y = -2x - 1 平行,
∴设直线 l 的函数表达式为 y = -2x + b,
∵直线 l 过点 P(1,4),∴ 4 = -2×1 + b,解得 b = 6,
∴直线 l 的函数表达式为 y = -2x + 6。
画出直线 l,如答图。
