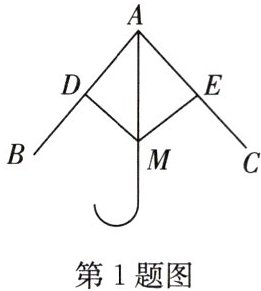
1. (2024·鼓楼区期中)如图是雨伞在开合过程中某时刻的截面图,伞骨$AB=AC$,点 D,E 分别是 AB,AC 的中点,DM,EM 是连接弹簧和伞骨的支架,且$DM=EM$,已知弹簧 M 在向上滑动的过程中,总有$\triangle ADM\cong \triangle AEM$,其判定依据是 (
A. ASA
B. AAS
C. SSS
D. SAS
C
)
A. ASA
B. AAS
C. SSS
D. SAS
答案:1.C
2. 如图,王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他要再钉上木条的根数至少是 (

A. 0根
B. 1根
C. 2根
D. 3根
B
)
A. 0根
B. 1根
C. 2根
D. 3根
答案:2.B
3. 如图,填空.(填“SSS”“SAS”“ASA”或“AAS”)

(1)已知$BD=CE,CD=BE$,利用
(2)已知$AD=AE,∠ADB=∠AEC$,利用
(3)已知$OE=OD,OB=OC$,利用
(4)已知$∠BEC=∠CDB,∠BCE=∠CBD$,利用

(1)已知$BD=CE,CD=BE$,利用
SSS
可以判定$\triangle BCD\cong \triangle CBE;$(2)已知$AD=AE,∠ADB=∠AEC$,利用
ASA
可以判定$\triangle ABD\cong \triangle ACE;$(3)已知$OE=OD,OB=OC$,利用
SAS
可以判定$\triangle BOE\cong \triangle COD;$(4)已知$∠BEC=∠CDB,∠BCE=∠CBD$,利用
AAS
可以判定$\triangle BCE\cong \triangle CBD.$答案:3.(1)SSS (2)ASA (3)SAS (4)AAS
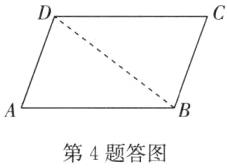
4. (2024·栖霞区月考)如图,在四边形 ABCD 中,$AB=CD,AD=CB$,求证:$∠A=∠C.$


答案:
4.证明:如答图,连接BD.
在△ADB和△CBD中,
$\left\{\begin{array}{l} AB=CD,\\ AD=CB,\\ DB=BD,\end{array}\right. $
∴△ADB≌△CBD(SSS),
∴∠A=∠C.
4.证明:如答图,连接BD.
在△ADB和△CBD中,
$\left\{\begin{array}{l} AB=CD,\\ AD=CB,\\ DB=BD,\end{array}\right. $
∴△ADB≌△CBD(SSS),
∴∠A=∠C.

5. 如图,$AB=AD,AC=AE,BC=DE$,点 E 在 BC 上.
(1)求证:$∠EAC=∠BAD;$
证明:在△ABC和△ADE中,
$\left\{\begin{array}{l} AB=AD,\\ AC=AE,\\ BC=DE,\end{array}\right.$
∴△ABC≌△ADE(
∴∠BAC=∠DAE,
∴∠BAC−∠BAE=∠DAE−∠BAE,
即∠EAC=∠BAD.
(2)若$∠EAC=42^{\circ }$,求$∠DEB$的度数.
解:∵△ABC≌△ADE,
∴∠ADE=∠ABC;
由(1)得∠BAD=∠EAC=
∵∠ADE+∠BAD=∠ABC+∠DEB,
∴∠DEB=∠BAD=
(1)求证:$∠EAC=∠BAD;$
证明:在△ABC和△ADE中,
$\left\{\begin{array}{l} AB=AD,\\ AC=AE,\\ BC=DE,\end{array}\right.$
∴△ABC≌△ADE(
SSS
),∴∠BAC=∠DAE,
∴∠BAC−∠BAE=∠DAE−∠BAE,
即∠EAC=∠BAD.
(2)若$∠EAC=42^{\circ }$,求$∠DEB$的度数.
解:∵△ABC≌△ADE,
∴∠ADE=∠ABC;
由(1)得∠BAD=∠EAC=
42°
,∵∠ADE+∠BAD=∠ABC+∠DEB,
∴∠DEB=∠BAD=
42°
.答案:5.(1)证明:在△ABC和△ADE中,
$\left\{\begin{array}{l} AB=AD,\\ AC=AE,\\ BC=DE,\end{array}\right. $
∴△ABC≌△ADE(SSS),
∴∠BAC=∠DAE,
∴∠BAC−∠BAE=∠DAE−∠BAE,
即∠EAC=∠BAD.
(2)解:∵△ABC≌△ADE,
∴∠ADE=∠ABC;
由(1)得∠BAD=∠EAC=42°,
∵∠ADE+∠BAD=∠ABC+∠DEB,
∴∠DEB=∠BAD=42°.
$\left\{\begin{array}{l} AB=AD,\\ AC=AE,\\ BC=DE,\end{array}\right. $
∴△ABC≌△ADE(SSS),
∴∠BAC=∠DAE,
∴∠BAC−∠BAE=∠DAE−∠BAE,
即∠EAC=∠BAD.
(2)解:∵△ABC≌△ADE,
∴∠ADE=∠ABC;
由(1)得∠BAD=∠EAC=42°,
∵∠ADE+∠BAD=∠ABC+∠DEB,
∴∠DEB=∠BAD=42°.