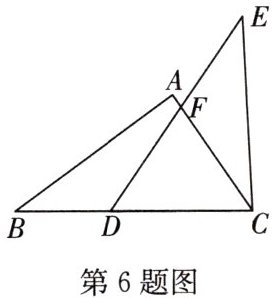
6. 如图,在$\triangle ABC$中,点 D,F 分别在边 BC,AC 上,若$BC=ED,AC=CD,AB=CE$,且$∠ACE=180^{\circ }-∠ABC-2α$.在下列角中,大小为α的是 ()

A.$∠CDF$
B.$∠ABC$
C.$∠CFD$
D.$∠CFE$

7. 如图,以$\triangle ABC$的顶点 A 为圆心,以 BC 长为半径作弧,再以顶点 C 为圆心,以 AB 长为半径作弧,两弧交于点 D,连接 AD,CD.若$∠B=65^{\circ }$,则$∠ADC$的度数为____.

8. 如图,已知$AB=AC,BD=CD$,若$∠A=60^{\circ },∠D=140^{\circ }$,则$∠B=$.

9. 如图,$AC=BC,AD=BD$,AB 与 CD 相交于点 O,下列结论:①$CO=DO$;②$AO=BO$;③$AB⊥CD$;④$\triangle ACO\cong \triangle BCO$.其中正确的是____.(填序号)

10. (2024·秦淮区期末)如图,已知$CD=BD$,点 E,F 分别是 CD,BD 的中点,$∠CAE=∠BAF,∠B=∠C$. 求证:
(1)$AE=AF;$
证明:(1)∵CD=BD,点E,F分别是CD,BD的中点，∴.
在△ACE和△ABF中,
$\left\{\begin{array}{l} ∠CAE=∠BAF,\\ ∠C=∠B,\\ CE=BF,\end{array}\right. $
∴△ACE≌△ABF(),
∴AE=AF.
(2)$\triangle ACD\cong \triangle ABD.$
证明:(2)∵△ACE≌△ABF,
∴,
在△ACD和△ABD中，
$\left\{\begin{array}{l} AC=AB,\\ AD=AD,\\ CD=BD,\end{array}\right. $
∴△ACD≌△ABD().

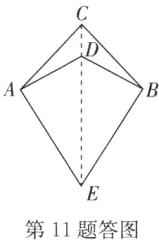
11. 如图,D 是四边形 AEBC 内一点,连接 AD,BD,已知$CA=CB,DA=DB,EA=EB$. 点 C,D,E 在一条直线上吗？为什么？