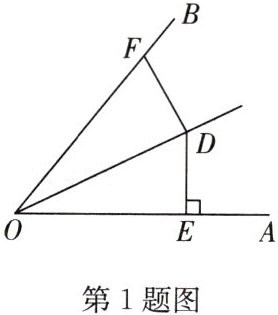
1. 如图,OD 平分∠AOB,DE⊥AO 于点 E,DE = 4.2,F 是射线 OB 上的任意一点,则 DF 的长度不可能是(
A. 4.2
B. 5.15
C. 3.69
D. 8
C
)
A. 4.2
B. 5.15
C. 3.69
D. 8
答案:C
2. 如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(

A. △ABC 三条中线的交点处
B. △ABC 三边的垂直平分线的交点处
C. △ABC 三条角平分线的交点处
D. △ABC 三条高所在直线的交点处
C
)
A. △ABC 三条中线的交点处
B. △ABC 三边的垂直平分线的交点处
C. △ABC 三条角平分线的交点处
D. △ABC 三条高所在直线的交点处
答案:C
3. 如图,在△ABC 中,AD 平分∠BAC,DE⊥AB. 若 AC = 2,DE = 1,则 $ S_{△ACD} $ =

1
.
答案:1
4. 如图,O 是△ABC 内一点,且点 O 到三边 AB,BC,CA 的距离 OF = OD = OE,若∠BAC = 80°,则∠BOC 的度数为______

130°
.
答案:$130^{\circ}$
5. 利用网格线画图. 如图,点 A,B,C 都在正方形网格的格点上.
(1)在 BC 上找一点 P,使点 P 到 AB 和 AC 的距离相等;
(2)在射线 AP 上找一点 Q,使 QB = QC.
(1)在 BC 上找一点 P,使点 P 到 AB 和 AC 的距离相等;
(2)在射线 AP 上找一点 Q,使 QB = QC.
答案:
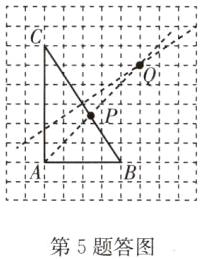
解: (1) 如答图, 点 $P$ 即为所求.
(2) 如答图, 点 $Q$ 即为所求.
解: (1) 如答图, 点 $P$ 即为所求.
(2) 如答图, 点 $Q$ 即为所求.

6. 如图,OC 是∠AOB 的平分线,P 是 OC 上一点,PD⊥OA,PE⊥OB,垂足分别为 D,E,点 F 是 OC 上的另一点,连接 DF,EF. 求证:DF = EF.
证明: ∵ OC 是∠AOB 的平分线, PD⊥OA, PE⊥OB,
∴
在 Rt△OPD 和 Rt△OPE 中, $\left\{\begin{array}{l} OP = OP, \\ PD = PE, \end{array}\right.$
∴ Rt△OPD ≌ Rt△OPE(
∵ OC 是∠AOB 的平分线, ∴
在△ODF 和△OEF 中, $\left\{\begin{array}{l} OD = OE, \\ ∠DOF = ∠EOF, \\ OF = OF, \end{array}\right.$
∴ △ODF ≌ △OEF(
证明: ∵ OC 是∠AOB 的平分线, PD⊥OA, PE⊥OB,
∴
PD = PE
.在 Rt△OPD 和 Rt△OPE 中, $\left\{\begin{array}{l} OP = OP, \\ PD = PE, \end{array}\right.$
∴ Rt△OPD ≌ Rt△OPE(
HL
), ∴ OD = OE
,∵ OC 是∠AOB 的平分线, ∴
∠DOF = ∠EOF
,在△ODF 和△OEF 中, $\left\{\begin{array}{l} OD = OE, \\ ∠DOF = ∠EOF, \\ OF = OF, \end{array}\right.$
∴ △ODF ≌ △OEF(
SAS
), ∴ DF = EF.答案:证明: $\because OP$ 是 $\angle AOB$ 的平分线, $PD \perp OA$, $PE \perp OB$,
$\therefore PD = PE$.
在 $Rt\triangle OPD$ 和 $Rt\triangle OPE$ 中, $\left\{\begin{array}{l} OP = OP, \\ PD = PE, \end{array}\right.$
$\therefore Rt\triangle OPD \cong Rt\triangle OPE(HL)$, $\therefore OD = OE$,
$\because OC$ 是 $\angle AOB$ 的平分线, $\therefore \angle DOF = \angle EOF$,
在 $\triangle ODF$ 和 $\triangle OEF$ 中, $\left\{\begin{array}{l} OD = OE, \\ \angle DOF = \angle EOF, \\ OF = OF, \end{array}\right.$
$\therefore \triangle ODF \cong \triangle OEF(SAS)$, $\therefore DF = EF$.
$\therefore PD = PE$.
在 $Rt\triangle OPD$ 和 $Rt\triangle OPE$ 中, $\left\{\begin{array}{l} OP = OP, \\ PD = PE, \end{array}\right.$
$\therefore Rt\triangle OPD \cong Rt\triangle OPE(HL)$, $\therefore OD = OE$,
$\because OC$ 是 $\angle AOB$ 的平分线, $\therefore \angle DOF = \angle EOF$,
在 $\triangle ODF$ 和 $\triangle OEF$ 中, $\left\{\begin{array}{l} OD = OE, \\ \angle DOF = \angle EOF, \\ OF = OF, \end{array}\right.$
$\therefore \triangle ODF \cong \triangle OEF(SAS)$, $\therefore DF = EF$.
7. (2023·滨海模拟)如图,AD//BC,AP,BP 分别平分∠DAB,∠ABC,CD 过点 P 且与 AD 垂直. 若 CD = 8,AB = 10,则△ABP 的面积为(

A. 20
B. 16
C. 40
D. 32
A
)
A. 20
B. 16
C. 40
D. 32
答案:A