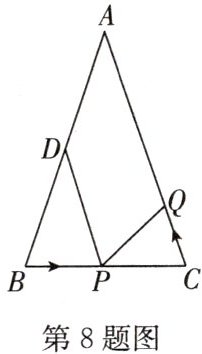
8. 如图,在$\triangle ABC$中,$AB = AC = 12$厘米,$\angle B = \angle C$,$BC = 8$厘米,点$D$为$AB$的中点. 如果点$P$在线段$BC$上以 2 厘米/秒的速度由$B$点向$C$点运动,同时,点$Q$在线段$CA$上由$C$点向$A$点运动. 若点$Q$的运动速度为$v$厘米/秒,则当$\triangle BPD$与$\triangle CQP$全等时,$v$的值为
2或3
.
答案:2或3
9. (14 分)(2023·陕西)如图,在$\triangle ABC$中,$\angle B = 50^{\circ}$,$\angle C = 20^{\circ}$. 过点$A$作$AE\perp BC$,垂足为$E$,延长$EA$至点$D$. 使$AD = AC$. 在边$AC$上截取$AF = AB$,连接$DF$. 求证:$DF = CB$.

证明:在△ABC中,∵∠B = 50°,∠C = 20°,
∴∠CAB = 180° - ∠B - ∠C =
∵AE⊥BC,∴∠AEC =
在△DAF和△CAB中,
$\begin{cases}AD = AC\\∠DAF = ∠CAB\\AF = AB\end{cases}$
∴△DAF≌△CAB(
∴DF = CB.

证明:在△ABC中,∵∠B = 50°,∠C = 20°,
∴∠CAB = 180° - ∠B - ∠C =
110°
.∵AE⊥BC,∴∠AEC =
90°
,∴∠DAF = ∠AEC + ∠C = 110°
,∴∠DAF = ∠CAB.在△DAF和△CAB中,
$\begin{cases}AD = AC\\∠DAF = ∠CAB\\AF = AB\end{cases}$
∴△DAF≌△CAB(
SAS
),∴DF = CB.
答案:证明:在△ABC中,∵∠B = 50°,∠C = 20°,
∴∠CAB = 180° - ∠B - ∠C = 110°.
∵AE⊥BC,∴∠AEC = 90°,∴∠DAF = ∠AEC + ∠C = 110°,∴∠DAF = ∠CAB.
在△DAF和△CAB中,
$\begin{cases}AD = AC\\∠DAF = ∠CAB\\AF = AB\end{cases}$
∴△DAF≌△CAB(SAS),
∴DF = CB.
∴∠CAB = 180° - ∠B - ∠C = 110°.
∵AE⊥BC,∴∠AEC = 90°,∴∠DAF = ∠AEC + ∠C = 110°,∴∠DAF = ∠CAB.
在△DAF和△CAB中,
$\begin{cases}AD = AC\\∠DAF = ∠CAB\\AF = AB\end{cases}$
∴△DAF≌△CAB(SAS),
∴DF = CB.
10. (16 分)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AD$平分$\angle CAB$,$DE\perp AB$于点$E$,点$F$在$AC$上,$BE = FC$. 求证:$BD = DF$.

证明:∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴
在△DCF和△DEB中,
$\begin{cases}DC = DE\\∠C = ∠BED\\CF = BE\end{cases}$
∴
∴BD = DF.

证明:∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴
DC = DE
.在△DCF和△DEB中,
$\begin{cases}DC = DE\\∠C = ∠BED\\CF = BE\end{cases}$
∴
△DCF≌△DEB(SAS)
,∴BD = DF.
答案:证明:∵AD平分∠BAC,DE⊥AB,∠C = 90°,
∴DC = DE.
在△DCF和△DEB中,
$\begin{cases}DC = DE\\∠C = ∠BED\\CF = BE\end{cases}$
∴△DCF≌△DEB(SAS),
∴BD = DF.
∴DC = DE.
在△DCF和△DEB中,
$\begin{cases}DC = DE\\∠C = ∠BED\\CF = BE\end{cases}$
∴△DCF≌△DEB(SAS),
∴BD = DF.
11. (22 分)如图,在四边形$ABDC$中,$\angle D = \angle B = 90^{\circ}$,点$O$为$BD$的中点,且$AO$平分$\angle BAC$. 求证:(1)$CO$平分$\angle ACD$; (2)$OA\perp OC$; (3)$AB + CD = AC$.


答案:
证明:(1)如答图,过点O作OE⊥AC于点E.
∵∠ABD = 90°,AO平分∠BAC,
∴OB = OE.
∵点O为BD的中点,
∴OB = OD,
∴OE = OD,
∴CO平分∠ACD.

(2)在Rt△ABO和Rt△AEO中,
$\begin{cases}AO = AO\\OB = OE\end{cases}$
∴Rt△ABO≌Rt△AEO(HL),∴∠AOB = ∠AOE,
同理求出∠COD = ∠COE,
∴∠AOC = ∠AOE + ∠COE = $\frac{1}{2}$×180° = 90°,
∴OA⊥OC.
(3)∵Rt△ABO≌Rt△AEO,∴AB = AE,
同理可得CD = CE,∵AC = AE + CE,∴AB + CD = AC;
证明:(1)如答图,过点O作OE⊥AC于点E.
∵∠ABD = 90°,AO平分∠BAC,
∴OB = OE.
∵点O为BD的中点,
∴OB = OD,
∴OE = OD,
∴CO平分∠ACD.

(2)在Rt△ABO和Rt△AEO中,
$\begin{cases}AO = AO\\OB = OE\end{cases}$
∴Rt△ABO≌Rt△AEO(HL),∴∠AOB = ∠AOE,
同理求出∠COD = ∠COE,
∴∠AOC = ∠AOE + ∠COE = $\frac{1}{2}$×180° = 90°,
∴OA⊥OC.
(3)∵Rt△ABO≌Rt△AEO,∴AB = AE,
同理可得CD = CE,∵AC = AE + CE,∴AB + CD = AC;