10. 在 $\triangle ABC$ 中, $CA = CB$, $\angle ACB = 120^{\circ}$,将一块足够大的三角尺 $PMN$ ($\angle M = 90^{\circ}$, $\angle MPN = 30^{\circ}$)按如图所示放置,顶点 $P$ 在线段 $AB$ 上滑动,三角尺的直角边 $PM$ 始终经过点 $C$,并且与 $CB$ 的夹角 $\angle PCB = \alpha$,斜边 $PN$ 交 $AC$ 于点 $D$. 在点 $P$ 的滑动过程中, $\triangle PCD$ 可以是等腰三角形吗? 若不可以,请说明理由;若可以,请求出夹角 $\alpha$ 的大小.
答:$\triangle PCD$可以是等腰三角形,夹角 $\alpha$ 的大小是
答:$\triangle PCD$可以是等腰三角形,夹角 $\alpha$ 的大小是
$0^{\circ}$或$45^{\circ}$或$90^{\circ}$
.答案:解:$\triangle PCD$可以是等腰三角形.由题意知$\angle PCA = 120^{\circ}-\alpha$,$\angle CPD = 30^{\circ}$.
①当$PC = PD$时,$\triangle PCD$是等腰三角形,$\angle PCD=\frac{1}{2}(180^{\circ}-\angle MPN)=\frac{1}{2}\times(180^{\circ}-30^{\circ}) = 75^{\circ}$,即$120^{\circ}-\alpha = 75^{\circ}$,解得$\alpha = 45^{\circ}$;
②当$PD = CD$时,$\triangle PCD$是等腰三角形,$\angle PCD=\angle CPD = 30^{\circ}$,即$120^{\circ}-\alpha = 30^{\circ}$,解得$\alpha = 90^{\circ}$;
③当$PC = CD$时,$\triangle PCD$是等腰三角形,$\angle PCD = 180^{\circ}-2\times30^{\circ}=120^{\circ}$,即$120^{\circ}-\alpha = 120^{\circ}$,解得$\alpha = 0^{\circ}$,此时点$P$与点$B$重合,点$D$与点$A$重合.
综上所述,当$\triangle PCD$是等腰三角形时,$\alpha$的大小是$45^{\circ}$或$90^{\circ}$或$0^{\circ}$.
①当$PC = PD$时,$\triangle PCD$是等腰三角形,$\angle PCD=\frac{1}{2}(180^{\circ}-\angle MPN)=\frac{1}{2}\times(180^{\circ}-30^{\circ}) = 75^{\circ}$,即$120^{\circ}-\alpha = 75^{\circ}$,解得$\alpha = 45^{\circ}$;
②当$PD = CD$时,$\triangle PCD$是等腰三角形,$\angle PCD=\angle CPD = 30^{\circ}$,即$120^{\circ}-\alpha = 30^{\circ}$,解得$\alpha = 90^{\circ}$;
③当$PC = CD$时,$\triangle PCD$是等腰三角形,$\angle PCD = 180^{\circ}-2\times30^{\circ}=120^{\circ}$,即$120^{\circ}-\alpha = 120^{\circ}$,解得$\alpha = 0^{\circ}$,此时点$P$与点$B$重合,点$D$与点$A$重合.
综上所述,当$\triangle PCD$是等腰三角形时,$\alpha$的大小是$45^{\circ}$或$90^{\circ}$或$0^{\circ}$.
11. (2023·吴江区月考)在边长为 9 的等边三角形 $ABC$ 中,点 $Q$ 是 $BC$ 上一点,点 $P$ 是 $AB$ 上一动点,以每秒 1 个单位长度的速度从点 $A$ 向点 $B$ 运动,设运动时间为 $t$ 秒.
(1)如图①,若 $BQ = 6$, $PQ // AC$,求 $t$ 的值;
(2)如图②,若点 $P$ 从点 $A$ 向点 $B$ 运动,同时点 $Q$ 以每秒 2 个单位长度的速度从点 $B$ 经点 $C$ 向点 $A$ 运动,连接 $PQ$, $AQ$,当 $t$ 为何值时, $\triangle APQ$ 为等边三角形?
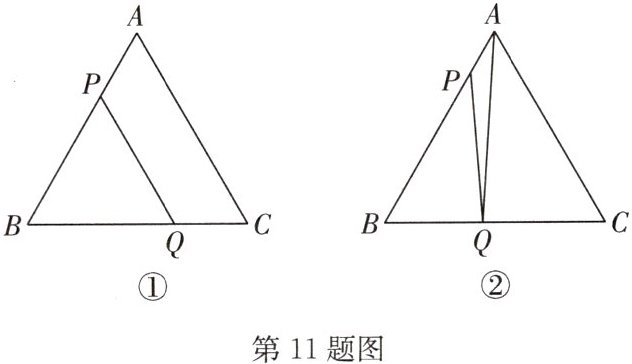
(1)如图①,若 $BQ = 6$, $PQ // AC$,求 $t$ 的值;
(2)如图②,若点 $P$ 从点 $A$ 向点 $B$ 运动,同时点 $Q$ 以每秒 2 个单位长度的速度从点 $B$ 经点 $C$ 向点 $A$ 运动,连接 $PQ$, $AQ$,当 $t$ 为何值时, $\triangle APQ$ 为等边三角形?

答案:
解:(1)$\because\triangle ABC$是等边三角形,$PQ// AC$,$\therefore\angle BQP=\angle C = 60^{\circ}$,$\angle BPQ=\angle A = 60^{\circ}$,又$\angle B = 60^{\circ}$,$\therefore\angle B=\angle BQP=\angle BPQ$,$\therefore\triangle BPQ$是等边三角形,$\therefore BP = BQ$.由题意可知,$AP = t$,则$BP = 9 - t$,$\therefore9 - t = 6$,解得$t = 3$,故$t$的值为3.
(2)①当点$Q$在边$BC$上时,$\angle BAQ\lt60^{\circ}$,$\triangle APQ$不可能为等边三角形;
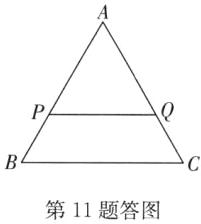
②当点$Q$在边$AC$上时,如答图,若$\triangle APQ$为等边三角形,则$AP = AQ$,由题意可知,$AP = t$,$BC + CQ = 2t$,$\therefore AQ = BC + AC-(BC + CQ)=9 + 9 - 2t = 18 - 2t$,$\therefore18 - 2t = t$,解得$t = 6$.
综上,当$t = 6$时,$\triangle APQ$为等边三角形.
解:(1)$\because\triangle ABC$是等边三角形,$PQ// AC$,$\therefore\angle BQP=\angle C = 60^{\circ}$,$\angle BPQ=\angle A = 60^{\circ}$,又$\angle B = 60^{\circ}$,$\therefore\angle B=\angle BQP=\angle BPQ$,$\therefore\triangle BPQ$是等边三角形,$\therefore BP = BQ$.由题意可知,$AP = t$,则$BP = 9 - t$,$\therefore9 - t = 6$,解得$t = 3$,故$t$的值为3.
(2)①当点$Q$在边$BC$上时,$\angle BAQ\lt60^{\circ}$,$\triangle APQ$不可能为等边三角形;
②当点$Q$在边$AC$上时,如答图,若$\triangle APQ$为等边三角形,则$AP = AQ$,由题意可知,$AP = t$,$BC + CQ = 2t$,$\therefore AQ = BC + AC-(BC + CQ)=9 + 9 - 2t = 18 - 2t$,$\therefore18 - 2t = t$,解得$t = 6$.
综上,当$t = 6$时,$\triangle APQ$为等边三角形.

12. 如图,在 $\triangle ABC$ 中, $AC = BC$, $\angle ACB = 90^{\circ}$,将 $\triangle ABC$ 绕点 $C$ 逆时针旋转 $\alpha$ 角 ($0^{\circ} < \alpha < 90^{\circ}$),得到 $\triangle A_1B_1C$,连接 $BB_1$,设 $CB_1$ 交 $AB$ 于点 $D$, $A_1B_1$ 分别交 $AB$, $AC$ 于点 $E$, $F$.
(1)求证: $\triangle CBD \cong \triangle CA_1F$;
(2)试用含 $\alpha$ 的代数式表示 $\angle B_1BD$;
(3)当 $\alpha$ 等于多少度时, $\triangle BB_1D$ 是等腰三角形?

(1)求证: $\triangle CBD \cong \triangle CA_1F$;
(2)试用含 $\alpha$ 的代数式表示 $\angle B_1BD$;
$45^{\circ}-\frac{\alpha}{2}$
(3)当 $\alpha$ 等于多少度时, $\triangle BB_1D$ 是等腰三角形?
$30^{\circ}$

答案:(1)证明:$\because AC = BC$,$\therefore\angle A=\angle ABC$.$\because\triangle ABC$绕点$C$逆时针旋转$\alpha$角$(0^{\circ}\lt\alpha\lt90^{\circ})$得到$\triangle A_{1}B_{1}C$,$\therefore\angle A_{1}=\angle A$,$A_{1}C = AC = BC$,$\angle ACA_{1}=\angle BCB_{1}=\alpha$,$\therefore\angle A_{1}=\angle CBD$.在$\triangle CBD$与$\triangle CA_{1}F$中,$\begin{cases}\angle CBD=\angle CA_{1}F,\\BC = A_{1}C,\\\angle BCD=\angle A_{1}CF,\end{cases}$$\therefore\triangle CBD\cong\triangle CA_{1}F(ASA)$.
(2)解:$\because$在$\triangle ABC$中,$AC = BC$,$\angle ACB = 90^{\circ}$,$\therefore\angle CAB=\angle CBA = 45^{\circ}$.又由旋转的性质得到$BC = B_{1}C$,$\therefore\angle CB_{1}B=\angle CBB_{1}=\frac{180^{\circ}-\alpha}{2}=90^{\circ}-\frac{\alpha}{2}$.$\therefore\angle B_{1}BD=\angle CBB_{1}-\angle CBA = 90^{\circ}-\frac{\alpha}{2}-45^{\circ}=45^{\circ}-\frac{\alpha}{2}$.
(3)解:由(2)知$\angle CBB_{1}=\angle CB_{1}B=\frac{1}{2}(180^{\circ}-\alpha)$,$\angle B_{1}BD = 45^{\circ}-\frac{\alpha}{2}$.由题意知$\angle B_{1}DB = 45^{\circ}+\alpha$.
①若$B_{1}B = B_{1}D$,则$\angle B_{1}DB=\angle B_{1}BD$,即$45^{\circ}+\alpha = 45^{\circ}-\frac{\alpha}{2}$,$\therefore\alpha = 0^{\circ}$(舍去);
②$\because\angle BB_{1}C=\angle B_{1}BC\gt\angle B_{1}BD$,$\therefore BD\gt B_{1}D$,即$BD\neq B_{1}D$;
③若$BB_{1} = BD$,则$\angle BDB_{1}=\angle BB_{1}D$,即$45^{\circ}+\alpha=\frac{1}{2}(180^{\circ}-\alpha)$,$\therefore\alpha = 30^{\circ}$.
由①②③可知,当$\alpha = 30^{\circ}$时,$\triangle BB_{1}D$为等腰三角形.
(2)解:$\because$在$\triangle ABC$中,$AC = BC$,$\angle ACB = 90^{\circ}$,$\therefore\angle CAB=\angle CBA = 45^{\circ}$.又由旋转的性质得到$BC = B_{1}C$,$\therefore\angle CB_{1}B=\angle CBB_{1}=\frac{180^{\circ}-\alpha}{2}=90^{\circ}-\frac{\alpha}{2}$.$\therefore\angle B_{1}BD=\angle CBB_{1}-\angle CBA = 90^{\circ}-\frac{\alpha}{2}-45^{\circ}=45^{\circ}-\frac{\alpha}{2}$.
(3)解:由(2)知$\angle CBB_{1}=\angle CB_{1}B=\frac{1}{2}(180^{\circ}-\alpha)$,$\angle B_{1}BD = 45^{\circ}-\frac{\alpha}{2}$.由题意知$\angle B_{1}DB = 45^{\circ}+\alpha$.
①若$B_{1}B = B_{1}D$,则$\angle B_{1}DB=\angle B_{1}BD$,即$45^{\circ}+\alpha = 45^{\circ}-\frac{\alpha}{2}$,$\therefore\alpha = 0^{\circ}$(舍去);
②$\because\angle BB_{1}C=\angle B_{1}BC\gt\angle B_{1}BD$,$\therefore BD\gt B_{1}D$,即$BD\neq B_{1}D$;
③若$BB_{1} = BD$,则$\angle BDB_{1}=\angle BB_{1}D$,即$45^{\circ}+\alpha=\frac{1}{2}(180^{\circ}-\alpha)$,$\therefore\alpha = 30^{\circ}$.
由①②③可知,当$\alpha = 30^{\circ}$时,$\triangle BB_{1}D$为等腰三角形.