1. 如图,用ASA来判定$\triangle ACD\cong \triangle ABE$,需要添加的条件是 (
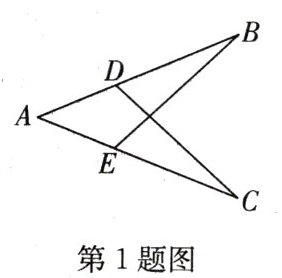
A. $∠AEB=∠ADC,∠C=∠B$
B. $∠AEB=∠ADC,CD=BE$
C. $AC=AB,AD=AE$
D. $AC=AB,∠C=∠B$
D
)
A. $∠AEB=∠ADC,∠C=∠B$
B. $∠AEB=∠ADC,CD=BE$
C. $AC=AB,AD=AE$
D. $AC=AB,∠C=∠B$
答案:D
2. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是 (
A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
C
)
A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
答案:C
3. (2024春·兴化期末)如图,点A为$\triangle ABC$和$\triangle ADE$的公共顶点,已知$∠C=∠E,AC=AE,$请你添加一个条件

∠BAC = ∠DAE(或∠CAD = ∠EAB)
,可以利用“ASA”判定$\triangle ABC\cong \triangle ADE$.(不再添加其他线条和字母)
答案:∠BAC = ∠DAE(或∠CAD = ∠EAB)
4. 如图,在$\triangle ABC$中,$∠CAD=∠EAD,∠ADC=∠ADE,CB=5cm,BD=3cm$,则ED的长为

2
cm.
答案:2
5. (2024春·海门区月考)如图,要测量河两岸相对两点A,B间的距离,在河岸BM上截取$BC=CD$,作$DE⊥BD$交AC的延长线于点E,垂足为点D,测得$ED=3,CD=4$,则A,B两点间的距离等于____

3
.
答案:3
6. (2024·惠山区一模)如图,点C在线段BD上,$AB⊥BD,ED⊥BD,$$∠ACB=∠CED,BC=DE.$
(1)求证:$\triangle ABC\cong \triangle CDE;$
证明:∵AB⊥BD,ED⊥BD,∴∠B = ∠D = 90°,
在△ABC和△CDE中,$\left\{\begin{array}{l} \angle B = \angle D, \\ BC = DE, \\ \angle ACB = \angle CED, \end{array}\right.$
∴△ABC≌△CDE(
(2)若$AB=2,DE=4$,求BD的长.
解:由(1)知△ABC≌△CDE,
∴AB = CD = 2,BC = DE = 4,
∴BD = BC + CD = 4 + 2 =

(1)求证:$\triangle ABC\cong \triangle CDE;$
证明:∵AB⊥BD,ED⊥BD,∴∠B = ∠D = 90°,
在△ABC和△CDE中,$\left\{\begin{array}{l} \angle B = \angle D, \\ BC = DE, \\ \angle ACB = \angle CED, \end{array}\right.$
∴△ABC≌△CDE(
ASA
)。(2)若$AB=2,DE=4$,求BD的长.
解:由(1)知△ABC≌△CDE,
∴AB = CD = 2,BC = DE = 4,
∴BD = BC + CD = 4 + 2 =
6
,即BD的长是6。
答案:(1)证明:∵AB⊥BD,ED⊥BD,∴∠B = ∠D = 90°,
在△ABC和△CDE中,$\left\{\begin{array}{l} \angle B = \angle D, \\ BC = DE, \\ \angle ACB = \angle CED, \end{array}\right.$
∴△ABC≌△CDE(ASA)。
(2)解:由(1)知△ABC≌△CDE,
∴AB = CD = 2,BC = DE = 4,
∴BD = BC + CD = 4 + 2 = 6,即BD的长是6。
在△ABC和△CDE中,$\left\{\begin{array}{l} \angle B = \angle D, \\ BC = DE, \\ \angle ACB = \angle CED, \end{array}\right.$
∴△ABC≌△CDE(ASA)。
(2)解:由(1)知△ABC≌△CDE,
∴AB = CD = 2,BC = DE = 4,
∴BD = BC + CD = 4 + 2 = 6,即BD的长是6。