7. 如图,长方形$OABC$的顶点$A$,$C$分别在坐标轴上,$B(8,7)$,$D(5,0)$,点$P$是边$AB$或边$BC$上的一点,连接$OP$,$DP$,当$\triangle ODP$为等腰三角形时,点$P$的坐标为
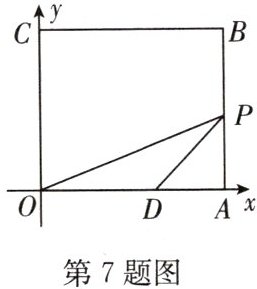
$(8,4)$或$(\frac{5}{2},7)$
.
答案:$(8,4)$或$(\frac{5}{2},7)$
8. 如图,方格纸中每个小正方形的边长都是1个单位长度,若学校位置的坐标为$A(1,2)$,解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆$(B)$位置的坐标;
(2)若体育馆位置的坐标为$C(-3,3)$,请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到$\triangle ABC$,求$\triangle ABC$的面积.

(1)请在图中建立适当的直角坐标系,并写出图书馆$(B)$位置的坐标;
(2)若体育馆位置的坐标为$C(-3,3)$,请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到$\triangle ABC$,求$\triangle ABC$的面积.

答案:
解:(1)建立直角坐标系如答图所示.

图书馆位置的坐标为$B(-3,-2)$.
(2)标出体育馆(C)的位置如答图所示,观察可得,$\triangle ABC$中BC边的长为5,BC边上的高为4,所以$\triangle ABC$的面积为$\frac{1}{2}×5×4=10$.
解:(1)建立直角坐标系如答图所示.

图书馆位置的坐标为$B(-3,-2)$.
(2)标出体育馆(C)的位置如答图所示,观察可得,$\triangle ABC$中BC边的长为5,BC边上的高为4,所以$\triangle ABC$的面积为$\frac{1}{2}×5×4=10$.
9. 如图是某台阶的一部分,并且每级台阶的宽等于高,每级台阶凸出的角的顶点记作$P_{k}$,$k$为正整数,点$P_{2}$的坐标为$(-1,0)$,点$P_{3}$的坐标为$(0,1)$.
(1)根据$P_{2}$,$P_{3}$两点的坐标,画出$x$轴、$y$轴,并标出原点$O$的位置.
(2)①直接用含$k$的代数式表示点$P_{k}$的坐标;
②判断点$(2025,2024)$是否在台阶上?并说明理由.
(3)把台阶上点$P_{k}$到$x$轴的距离与点$P_{k}$到$y$轴的距离中的较小值称为$P_{k}$的“短距”,若台阶中某一点$P_{k}$的“短距”为1,直接写出该点的坐标.

(1)根据$P_{2}$,$P_{3}$两点的坐标,画出$x$轴、$y$轴,并标出原点$O$的位置.
(2)①直接用含$k$的代数式表示点$P_{k}$的坐标;
②判断点$(2025,2024)$是否在台阶上?并说明理由.
(3)把台阶上点$P_{k}$到$x$轴的距离与点$P_{k}$到$y$轴的距离中的较小值称为$P_{k}$的“短距”,若台阶中某一点$P_{k}$的“短距”为1,直接写出该点的坐标.

答案:
解:(1)画出x轴、y轴,并标出原点O的位置如答图所示.

(2)①$P_{k}(k - 3,k - 2)$(k为正整数).
②不在.理由:当$k - 3 = 2025$时,$k = 2028$,则$k - 2 = 2028 - 2 = 2026≠2024$,∴点$(2025,2024)$不在台阶上.
(3)$P_{1}(-2,-1)$,$P_{4}(1,2)$.
解:(1)画出x轴、y轴,并标出原点O的位置如答图所示.

(2)①$P_{k}(k - 3,k - 2)$(k为正整数).
②不在.理由:当$k - 3 = 2025$时,$k = 2028$,则$k - 2 = 2028 - 2 = 2026≠2024$,∴点$(2025,2024)$不在台阶上.
(3)$P_{1}(-2,-1)$,$P_{4}(1,2)$.