9. 如图,两条互相垂直的直线$m,n交于点O$,一块等腰直角三角尺的直角顶点$A在直线m$上,锐角顶点$B在直线n$上,$D是斜边BC$的中点. 已知$OD= \sqrt{7}$,$BC= 4$,则$S_{\triangle AOB}= $
$\frac{3}{2}$
.答案:$\frac{3}{2}$
10. (10分)(1)计算:$\sqrt{121}-\sqrt{49}+\sqrt[3]{27}$; (2)求$x$的值:$4(x-1)^{2}= 25$.
答案:解:(1) $\sqrt{121}$ - $\sqrt{49}$ + $\sqrt[3]{27}$ = 11 - 7 + 3 = 7.
(2)∵4(x - 1)² = 25,∴(x - 1)² = $\frac{25}{4}$,∴x - 1 = ±2.5,解得x = 3.5或x = -1.5.
(2)∵4(x - 1)² = 25,∴(x - 1)² = $\frac{25}{4}$,∴x - 1 = ±2.5,解得x = 3.5或x = -1.5.
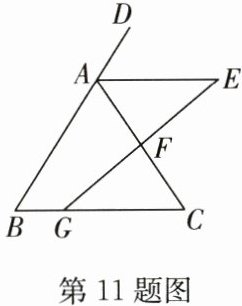
11. (10分)如图,已知$\triangle ABC$,点$D在线段AB$的反向延长线上,过$AC的中点F作线段GE交∠DAC的平分线于点E$,交$BC于点G$,且$AE// BC$.
(1)求证:$\triangle ABC$是等腰三角形;
(2)若$AE= 8$,$AB= 10$,$GC= 2BG$,求$\triangle ABC$的周长.
(1)求证:$\triangle ABC$是等腰三角形;
(2)若$AE= 8$,$AB= 10$,$GC= 2BG$,求$\triangle ABC$的周长.

答案:(1)证明:∵AE//BC,∴∠B = ∠DAE,∠C = ∠CAE;∵AE平分∠DAC,∴∠DAE = ∠CAE.∴∠B = ∠C;∴AB = AC;∴△ABC是等腰三角形.
(2)解:∵F是AC的中点,∴AF = CF.
∵AE//BC,∴∠C = ∠CAE.
由对顶角相等可知:∠AFE = ∠GFC;
在△AFE和△CFG中, $\begin{cases} \angle CAE = \angle C \\ AF = FC \\ \angle AFE = \angle GFC \end{cases}$
∴△AFE≌△CFG(ASA).∴AE = GC = 8.
∵GC = 2BG,∴BG = 4.∴BC = 12.
∴△ABC的周长 = AB + AC + BC = 10 + 10 + 12 = 32.
(2)解:∵F是AC的中点,∴AF = CF.
∵AE//BC,∴∠C = ∠CAE.
由对顶角相等可知:∠AFE = ∠GFC;
在△AFE和△CFG中, $\begin{cases} \angle CAE = \angle C \\ AF = FC \\ \angle AFE = \angle GFC \end{cases}$
∴△AFE≌△CFG(ASA).∴AE = GC = 8.
∵GC = 2BG,∴BG = 4.∴BC = 12.
∴△ABC的周长 = AB + AC + BC = 10 + 10 + 12 = 32.
12. (12分)甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地. 如图,线段$OA表示货车离甲地的路程y$(千米)与所用时间$x$(时)之间的函数关系,折线$BCD表示轿车离甲地的路程y$(千米)与$x$(时)之间的函数关系. 根据图象解答下列问题:
(1)求线段$CD$对应的函数表达式;
(2)在轿车追上货车后到达乙地前,何时轿车在货车前30千米?

(1)求线段$CD$对应的函数表达式;
(2)在轿车追上货车后到达乙地前,何时轿车在货车前30千米?

答案:解:(1)设线段CD对应的函数表达式为y = kx + b.
将C(2,100),D(4.5,400)代入y = kx + b中,得
$\begin{cases} 2k + b = 100 \\ 4.5k + b = 400 \end{cases}$,解得$\begin{cases} k = 120 \\ b = -140 \end{cases}$.
所以线段CD对应的函数表达式为y = 120x - 140(2≤x≤4.5).
(2)根据题意得,线段OA对应的函数表达式为y = 80x,则120x - 140 - 80x = 30,解得x = $\frac{17}{4}$.
答:当x = $\frac{17}{4}$时,轿车在货车前30千米.
将C(2,100),D(4.5,400)代入y = kx + b中,得
$\begin{cases} 2k + b = 100 \\ 4.5k + b = 400 \end{cases}$,解得$\begin{cases} k = 120 \\ b = -140 \end{cases}$.
所以线段CD对应的函数表达式为y = 120x - 140(2≤x≤4.5).
(2)根据题意得,线段OA对应的函数表达式为y = 80x,则120x - 140 - 80x = 30,解得x = $\frac{17}{4}$.
答:当x = $\frac{17}{4}$时,轿车在货车前30千米.
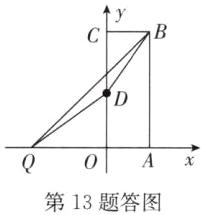
13. (14分)如图,在平面直角坐标系中,$O$为坐标原点,长方形$OABC$中,点$B的坐标为(3,8)$,点$A,C$分别在坐标轴上,$D为OC$的中点.
(1)在$x轴上找一点P$,使得$PD+PB$最小,则点$P$的坐标为______;
(2)在$x轴上找一点Q$,使得$|QD-QB|$最大,求出点$Q$的坐标.

(1)在$x轴上找一点P$,使得$PD+PB$最小,则点$P$的坐标为______;
(2)在$x轴上找一点Q$,使得$|QD-QB|$最大,求出点$Q$的坐标.

答案:
(1)(1,0)
(2)解:如答图.根据三角形两边之差小于第三边,得当B,D,Q
三点在同一直线上时,|QD - QB| = BD最大.
设直线BD的函数表达式为y = ax + c,则
$\begin{cases} 3a + c = 8 \\ c = 4 \end{cases}$,解得$\begin{cases} a = \frac{4}{3} \\ c = 4 \end{cases}$
∴直线BD:y = $\frac{4}{3}$x + 4.
当$\frac{4}{3}$x + 4 = 0时,解得x = -3,∴点Q(-3,0).
(1)(1,0)
(2)解:如答图.根据三角形两边之差小于第三边,得当B,D,Q
三点在同一直线上时,|QD - QB| = BD最大.
设直线BD的函数表达式为y = ax + c,则
$\begin{cases} 3a + c = 8 \\ c = 4 \end{cases}$,解得$\begin{cases} a = \frac{4}{3} \\ c = 4 \end{cases}$
∴直线BD:y = $\frac{4}{3}$x + 4.
当$\frac{4}{3}$x + 4 = 0时,解得x = -3,∴点Q(-3,0).
