1. 函数 $ y = ( 3 m + 5 ) x - m $ 是关于 $ x $ 的一次函数,且 $ y $ 随 $ x $ 的增大而减小,求 $ m $ 的取值范围,并指出该函数图象经过哪些象限.
答案:解:∵y=(3m+5)x−m是关于x的一次函数,且y随x
的增大而减小,
∴3m+5<0,解得m<−$\frac{5}{3}$.∴−m>$\frac{5}{3}$,
∴该函数图象经过第一、二、四象限.
的增大而减小,
∴3m+5<0,解得m<−$\frac{5}{3}$.∴−m>$\frac{5}{3}$,
∴该函数图象经过第一、二、四象限.
2. 画出 $ y = 2 x - 4 $ 的图象,确定 $ x $ 取何值时:(1) $ y > 0 $;(2) $ y < - 4 $.

答案:
解:当x=0时,y=−4,
当y=0时,2x−4=0,解得x=2,
∴函数图象与两坐标轴的交点为(0,−4),(2,0).
图象如答图.
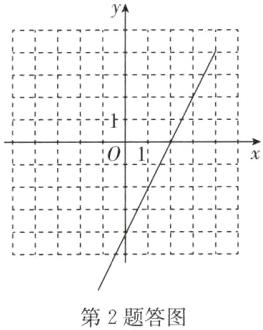
(1)当x>2时,y>0.
(2)当x<0时,y<−4.
解:当x=0时,y=−4,
当y=0时,2x−4=0,解得x=2,
∴函数图象与两坐标轴的交点为(0,−4),(2,0).
图象如答图.

(1)当x>2时,y>0.
(2)当x<0时,y<−4.
3. 已知一次函数 $ y = ( 3 - m ) x + 2 m - 9 $ 的图象与 $ y $ 轴的负半轴相交,$ y $ 随 $ x $ 的增大而减小,且 $ m $ 为整数.
(1) 求 $ m $ 的值;
(2) 当 $ - 1 \leq x \leq 2 $ 时,求 $ y $ 的取值范围.
(1) 求 $ m $ 的值;
(2) 当 $ - 1 \leq x \leq 2 $ 时,求 $ y $ 的取值范围.
答案:解:(1)∵一次函数y=(3−m)x+2m−9的图象与y轴的负半轴相交,y随x的增大而减小,
∴$\begin{cases}3 - m < 0,\\2m - 9 < 0,\end{cases}$解得3<m<4.5.
∵m为整数,∴m=4.
(2)由(1)知m=4,则该一次函数的表达式为y=−x−1.
∵ - 1 ≤ x ≤ 2,∴ - 3 ≤ - x - 1 ≤ 0,
即y的取值范围是 - 3 ≤ y ≤ 0.
∴$\begin{cases}3 - m < 0,\\2m - 9 < 0,\end{cases}$解得3<m<4.5.
∵m为整数,∴m=4.
(2)由(1)知m=4,则该一次函数的表达式为y=−x−1.
∵ - 1 ≤ x ≤ 2,∴ - 3 ≤ - x - 1 ≤ 0,
即y的取值范围是 - 3 ≤ y ≤ 0.
4. 已知一次函数 $ y = - 2 x - 2 $.
(1) 根据关系式在如图所示坐标系中画出函数的图象;
(2) 求出图象与 $ x $ 轴、$ y $ 轴的交点 $ A $,$ B $ 的坐标;
(3) 求 $ A $,$ B $ 两点间的距离;
(4) 求 $ \triangle A O B $ 的面积;
(5) $ y $ 的值随 $ x $ 值的增大怎样变化?

(1) 根据关系式在如图所示坐标系中画出函数的图象;
(2) 求出图象与 $ x $ 轴、$ y $ 轴的交点 $ A $,$ B $ 的坐标;
(3) 求 $ A $,$ B $ 两点间的距离;
(4) 求 $ \triangle A O B $ 的面积;
(5) $ y $ 的值随 $ x $ 值的增大怎样变化?

答案:
解:(1)如答图.

(2)当y=0时,−2x−2=0,解得x=−1,即A(−1,0);当x=0时,y=−2,即B(0,−2).
(3)由勾股定理得AB=$\sqrt{1^{2}+2^{2}}$=$\sqrt{5}$
(4)S△AOB=$\frac{1}{2}$×1×2=1.
(5)由图象可知y的值随x值的增大而减小.
解:(1)如答图.

(2)当y=0时,−2x−2=0,解得x=−1,即A(−1,0);当x=0时,y=−2,即B(0,−2).
(3)由勾股定理得AB=$\sqrt{1^{2}+2^{2}}$=$\sqrt{5}$
(4)S△AOB=$\frac{1}{2}$×1×2=1.
(5)由图象可知y的值随x值的增大而减小.