13. 在一次爆破中,用一条$96cm$长的引火线来使装在钻孔里的炸药爆炸,引火线燃烧的速度是$0.8cm/s$,点火者点燃引火线后以$5m/s$的速度跑开.
(1)这条引火线完全燃烧引爆炸药需要多少秒?
(2)请计算后回答人能不能在爆炸前跑到离爆炸点$500m$远的安全区?
(1)这条引火线完全燃烧引爆炸药需要多少秒?
(2)请计算后回答人能不能在爆炸前跑到离爆炸点$500m$远的安全区?
答案:13. (1)这条引火线完全燃烧引爆炸药需要多少秒?由$v=\frac {s}{t}$可得,这条引火线完全燃烧引爆炸药需要的时间$t_{1}=\frac {s_{1}}{v_{1}}=\frac {96cm}{0.8cm/s}=120s$(2)请计算后回答人能不能在爆炸前跑到离爆炸点$500m$远的安全区?方法一:人跑到安全区需用的时间$t_{2}=\frac {s_{2}}{v_{2}}=\frac {500m}{5m/s}=100s$由$t_{2}\lt t_{1}$可知,人能跑到安全区.方法二:人在$t_{1}$时间内通过的路程$s_{2}=v_{2}t_{1}=5m/s×120s=600m>500m$所以,人能跑到安全区.方法三:人跑到安全区所需的时间$t_{2}=\frac {s_{2}}{v_{2}}=\frac {500m}{5m/s}=100s$经过 100 s 引火线燃烧的长度$L=v_{1}t_{2}=0.8cm/s×100s=80cm<96cm$所以,人能跑到安全区.
解析:
(1)由$v = \frac{s}{t}$可得,引火线完全燃烧所需时间$t_{1}=\frac{s_{1}}{v_{1}}=\frac{96\space cm}{0.8\space cm/s}=120\space s$。
(2)方法一:人跑到安全区所需时间$t_{2}=\frac{s_{2}}{v_{2}}=\frac{500\space m}{5\space m/s}=100\space s$,因为$t_{2}=100\space s\lt t_{1}=120\space s$,所以人能跑到安全区。
方法二:人在$t_{1}=120\space s$内跑的路程$s = v_{2}t_{1}=5\space m/s×120\space s = 600\space m$,因为$600\space m\gt500\space m$,所以人能跑到安全区。
方法三:人跑到安全区需$t_{2}=100\space s$,此时引火线燃烧长度$L = v_{1}t_{2}=0.8\space cm/s×100\space s = 80\space cm$,因为$80\space cm\lt96\space cm$,所以人能跑到安全区。
(以上方法任选其一即可)
(2)方法一:人跑到安全区所需时间$t_{2}=\frac{s_{2}}{v_{2}}=\frac{500\space m}{5\space m/s}=100\space s$,因为$t_{2}=100\space s\lt t_{1}=120\space s$,所以人能跑到安全区。
方法二:人在$t_{1}=120\space s$内跑的路程$s = v_{2}t_{1}=5\space m/s×120\space s = 600\space m$,因为$600\space m\gt500\space m$,所以人能跑到安全区。
方法三:人跑到安全区需$t_{2}=100\space s$,此时引火线燃烧长度$L = v_{1}t_{2}=0.8\space cm/s×100\space s = 80\space cm$,因为$80\space cm\lt96\space cm$,所以人能跑到安全区。
(以上方法任选其一即可)
14. 喜羊羊发现后方$100m处的灰太狼正以16m/s$的速度向自己猛扑过来,此时喜羊羊与前方的羊村相距$300m$.喜羊羊马上以$12.5m/s$的最快速度向羊村跑去,问:喜羊羊能否安全跑进羊村? (请用两种不同方法通过计算加以说明)
答案:14. 喜羊羊能否安全跑进羊村? (请用两种不同方法通过计算加以说明)方法一:由$v=\frac {s}{t}$可知,喜羊羊跑到羊村的时间$t_{1}=\frac {s_{1}}{v_{1}}=\frac {300m}{12.5m/s}=24s$灰太狼跑到羊村的时间$t_{2}=\frac {s_{2}}{v_{2}}=\frac {300m+100m}{16m/s}=25s$由于$t_{1}\lt t_{2}$,所以喜羊羊能安全跑到羊村.方法二:由$v=\frac {s}{t}$可知,喜羊羊跑到羊村的时间$t_{1}=\frac {s_{1}}{v_{1}}=\frac {300m}{12.5m/s}=24s$当喜羊羊跑到羊村时,灰太狼通过的路程$s_{2}=v_{2}t_{1}=16m/s×24s=384m$由于灰太狼通过的路程小于灰太狼到羊村的距离,所以喜羊羊能安全跑进羊村.
解析:
方法一:
由$v = \frac{s}{t}$可得,喜羊羊跑到羊村的时间$t_{1}=\frac{s_{1}}{v_{1}}=\frac{300m}{12.5m/s}=24s$。
灰太狼到羊村的距离为$300m + 100m=400m$,其跑到羊村的时间$t_{2}=\frac{s_{2}}{v_{2}}=\frac{400m}{16m/s}=25s$。
因为$t_{1}<t_{2}$,所以喜羊羊能安全跑进羊村。
方法二:
由$v = \frac{s}{t}$可得,喜羊羊跑到羊村的时间$t_{1}=\frac{s_{1}}{v_{1}}=\frac{300m}{12.5m/s}=24s$。
在$t_{1}=24s$内,灰太狼跑的路程$s_{2}=v_{2}t_{1}=16m/s×24s = 384m$。
灰太狼到羊村的距离为$400m$,因为$384m<400m$,所以喜羊羊能安全跑进羊村。
由$v = \frac{s}{t}$可得,喜羊羊跑到羊村的时间$t_{1}=\frac{s_{1}}{v_{1}}=\frac{300m}{12.5m/s}=24s$。
灰太狼到羊村的距离为$300m + 100m=400m$,其跑到羊村的时间$t_{2}=\frac{s_{2}}{v_{2}}=\frac{400m}{16m/s}=25s$。
因为$t_{1}<t_{2}$,所以喜羊羊能安全跑进羊村。
方法二:
由$v = \frac{s}{t}$可得,喜羊羊跑到羊村的时间$t_{1}=\frac{s_{1}}{v_{1}}=\frac{300m}{12.5m/s}=24s$。
在$t_{1}=24s$内,灰太狼跑的路程$s_{2}=v_{2}t_{1}=16m/s×24s = 384m$。
灰太狼到羊村的距离为$400m$,因为$384m<400m$,所以喜羊羊能安全跑进羊村。
15. 如图所示,电视节目中“闯关游戏”的笔直通道上每隔$8m$设有一个关卡,各关卡同步放行和关闭,放行和关闭时间分别为$5s和2s$,关卡关闭时,人能在两关卡间运动,但不能通过关卡;当小强正通过关卡$1左侧9m远的A$处时,关卡刚好放行,若他全程以$2m/s$的速度运动,则最先挡住他前进的关卡是 (
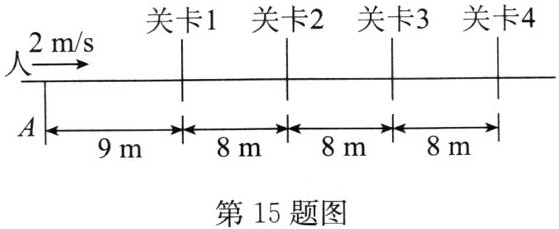
A.关卡$4$
B.关卡$3$
C.关卡$2$
D.关卡$1$
B
)
A.关卡$4$
B.关卡$3$
C.关卡$2$
D.关卡$1$
答案:15. B
解析:
解:
1. 通过关卡1:
距离:9m,速度:2m/s,时间$ t_1=\frac{9}{2}=4.5s $。
关卡放行时间5s,$ 4.5s<5s $,可通过。
2. 通过关卡2:
关卡1到关卡2距离8m,时间$ t_2=\frac{8}{2}=4s $,总时间$ t_{\text{总1}}=4.5+4=8.5s $。
关卡周期7s(5s放行+2s关闭),$ 8.5s-7s=1.5s $(处于下一轮放行中),可通过。
3. 通过关卡3:
关卡2到关卡3距离8m,时间$ t_3=\frac{8}{2}=4s $,总时间$ t_{\text{总2}}=8.5+4=12.5s $。
周期数:$ 12.5÷7=1$(周期)余$ 5.5s $,$ 5.5s>5s $(已关闭),不可通过。
最先挡住的是关卡3。
答案:B
1. 通过关卡1:
距离:9m,速度:2m/s,时间$ t_1=\frac{9}{2}=4.5s $。
关卡放行时间5s,$ 4.5s<5s $,可通过。
2. 通过关卡2:
关卡1到关卡2距离8m,时间$ t_2=\frac{8}{2}=4s $,总时间$ t_{\text{总1}}=4.5+4=8.5s $。
关卡周期7s(5s放行+2s关闭),$ 8.5s-7s=1.5s $(处于下一轮放行中),可通过。
3. 通过关卡3:
关卡2到关卡3距离8m,时间$ t_3=\frac{8}{2}=4s $,总时间$ t_{\text{总2}}=8.5+4=12.5s $。
周期数:$ 12.5÷7=1$(周期)余$ 5.5s $,$ 5.5s>5s $(已关闭),不可通过。
最先挡住的是关卡3。
答案:B