(1) 在括号里填“直线”“射线”或“线段”。
① 两点之间的连线中,(
② 能量出(
① 两点之间的连线中,(
线段
)的长度最短。② 能量出(
线段
)的长度,(直线
)没有端点,(射线
)只有一端是无限延伸的。答案: (1) ① 线段 ② 线段 直线 射线
(2)(南通真题)如左下图,钟面上的分针从“12”开始走 15 分钟,形成的是(

直
)角,是(90
)°;从“12”开始走 30 分钟,形成的是(平
)角,是(180
)°。
答案:(2) 直 90 平 180
(3) 如右上图,长方形纸经过折叠后,$∠3= 40^{\circ },∠4= $(
25
)°。答案: (3) 25
(1) 直线外一点到直线之间,(
A.线段
B.垂线
C.垂直线段
C
)最短。A.线段
B.垂线
C.垂直线段
答案:解析:本题考查点到直线的距离的定义。
点到直线的距离是指从直线外一点到这条直线的垂线段的长度。
在直线外一点与直线上各点的连线中,垂线段最短。
答案:C。
点到直线的距离是指从直线外一点到这条直线的垂线段的长度。
在直线外一点与直线上各点的连线中,垂线段最短。
答案:C。
(2) 甲、乙、丙是同一平面内的三条直线,甲和乙都是丙的平行线,甲和乙互相(
A.平行
B.垂直
C.无法确定
A
)。A.平行
B.垂直
C.无法确定
答案:解析:
题目考查了平行线的性质及平行公理的推论。
在同一平面内,如果两条直线都与同一条直线平行,那么这两条直线也互相平行。
因为甲和乙都是丙的平行线,所以甲和乙互相平行。
答案:A。
题目考查了平行线的性质及平行公理的推论。
在同一平面内,如果两条直线都与同一条直线平行,那么这两条直线也互相平行。
因为甲和乙都是丙的平行线,所以甲和乙互相平行。
答案:A。
3. 分别量出两个平行四边形中$∠1$、$∠2的度数和∠3$、$∠4$的度数。你有什么发现?


答案:3. 左图:$\angle 1=30^{\circ },\angle 2=30^{\circ },\angle 3=20^{\circ },\angle 4=20^{\circ }$ 右图:$\angle 1=90^{\circ },\angle 2=90^{\circ },\angle 3=40^{\circ },\angle 4=40^{\circ }$ 发现:$\angle 1=\angle 2,\angle 3=\angle 4$
4. 在下面的图形中,哪些线段是互相垂直的? 请标出垂直符号。哪些线段是互相平行的? 请用相同颜色的彩笔描一描。


答案:
4.
4.
解析:
(因无具体图形,无法准确标注垂直符号及平行线段。若图形为常见几何图形,如第一个为直角梯形,则垂直线段为梯形的上底与直角腰、下底与直角腰,在相交处标垂直符号“⊥”;第二个正六边形对边平行,用相同颜色描对边;第三个三角形若含直角,则直角边互相垂直,标“⊥”。具体需根据实际图形判断。)
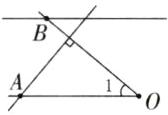
5.(南通真题)根据要求在下图中量一量,画一画。

(1) 用量角器量出$∠1$是( )°。
(2) 过点 A 画出边 OB 的垂线。
(3) 过点 B 画出边 OA 的平行线。

(1) 用量角器量出$∠1$是( )°。
(2) 过点 A 画出边 OB 的垂线。
(3) 过点 B 画出边 OA 的平行线。
答案:
5. (1) 40 (2) 如图 (3) 如图
5. (1) 40 (2) 如图 (3) 如图

6.(思维过程)如图,$∠1+∠2+∠3= 220^{\circ },∠1$是多少度?


答案:6. $220^{\circ }-180^{\circ }=40^{\circ }$
解析:观察题图,我们可以看出$∠2$和$∠3$合起来是一个平角,因此可以用$∠1$、$∠2$、$∠3$的度数之和减去$∠2$、$∠3$的度数之和,从而求出$∠1$的度数。
解析:观察题图,我们可以看出$∠2$和$∠3$合起来是一个平角,因此可以用$∠1$、$∠2$、$∠3$的度数之和减去$∠2$、$∠3$的度数之和,从而求出$∠1$的度数。