(1)(南通海安)用量角器去量一个$60^{\circ }$的角,量角器的中心与角的顶点重合。如果角的一边与外圈$180^{\circ }$刻度线重合,那么另外一条边将与外圈(
120
)$^{\circ }$刻度线重合;如果角的一条边与外圈$40^{\circ }$刻度线重合,那么另一条边将与外圈(100
)$^{\circ }$刻度线重合。答案:120 100
解析:
解:
1. 当角的一边与外圈$180^{\circ}$刻度线重合时,另一条边与外圈刻度线重合的度数为:$180^{\circ}-60^{\circ}=120^{\circ}$
2. 当角的一条边与外圈$40^{\circ}$刻度线重合时,另一条边与外圈刻度线重合的度数为:$40^{\circ}+60^{\circ}=100^{\circ}$
120;100
1. 当角的一边与外圈$180^{\circ}$刻度线重合时,另一条边与外圈刻度线重合的度数为:$180^{\circ}-60^{\circ}=120^{\circ}$
2. 当角的一条边与外圈$40^{\circ}$刻度线重合时,另一条边与外圈刻度线重合的度数为:$40^{\circ}+60^{\circ}=100^{\circ}$
120;100
(2)(淮安洪泽区)选择“前面”“右面”或“上面”填空。

上面
前面
右面
答案:上面 前面 右面
(3)(南通海门区)写出下面角的度数。
分针走一大格,形成的角是(
一副三角尺拼成的角是(
用一张正方形纸折出的角是(

分针走一大格,形成的角是(
30
)$^{\circ }$。
一副三角尺拼成的角是(
120
)$^{\circ }$。
用一张正方形纸折出的角是(
135
)$^{\circ }$。
答案:30 120 135
(4)(镇江丹徒区)用3个同样大的正方体摆一个物体,从上面看到的是,有(
2
)种不同的摆法;从前面看到的是,有(4
)种不同的摆法。(每个正方体至少有一个面与其他正方体的面重合)答案:2 4
① 如图,把一副三角尺按两种方式拼在一起,$∠1=$(
② 如图,将一张圆形纸片对折三次,$∠3=$(
③ 如图,点A到直线a的距离是线段(
135
)$^{\circ },∠2=$(15
)$^{\circ }$。② 如图,将一张圆形纸片对折三次,$∠3=$(
45
)$^{\circ }$。③ 如图,点A到直线a的距离是线段(
AD
)的长度。答案:① 135 15 ② 45 ③ AD
(6)(扬州江都区)如左下图,在正方形ABCD中,两条对角线相交于点O。如果点O到线段AB的距离是3厘米,那么正方形的周长是(
24
)厘米,面积是(36
)平方厘米。答案:24 36
解析:
在正方形ABCD中,对角线AC、BD相交于点O。
∵正方形对角线互相平分且相等,O为AC、BD中点,
∴点O到AB的距离等于正方形边长的一半(O到AB的垂线段为△AOB的高,等于边长的1/2)。
设正方形边长为a,由题意得:a/2 = 3厘米,解得a = 6厘米。
周长:4a = 4×6 = 24厘米。
面积:a² = 6² = 36平方厘米。
24 36
∵正方形对角线互相平分且相等,O为AC、BD中点,
∴点O到AB的距离等于正方形边长的一半(O到AB的垂线段为△AOB的高,等于边长的1/2)。
设正方形边长为a,由题意得:a/2 = 3厘米,解得a = 6厘米。
周长:4a = 4×6 = 24厘米。
面积:a² = 6² = 36平方厘米。
24 36
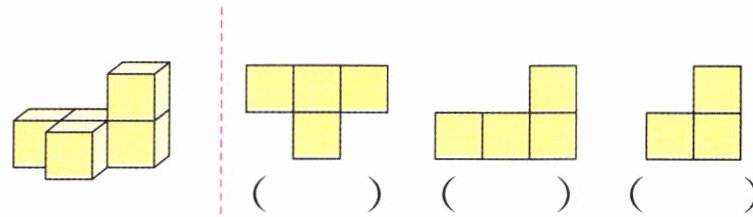
(7)(无锡江阴)右上图的物体由
7
个同样大的正方体摆成,至少再添加11
个这样的正方体就能使这个物体成为一个大长方体。答案:7 11
解析:
解:该物体由7个同样大的正方体摆成。要使其成为大长方体,假设大长方体的长、宽、高分别为3、3、2(根据常见摆法推测),则大长方体所需正方体总数为3×3×2=18个,至少再添加18-7=11个。
7 11
7 11