(1)(南通启东)小虎在计算$54÷9×(75+□)$时,漏抄了题中的括号,然后按四则运算的顺序计算,得到的结果是 498。正确的结果是(
738
)。答案：738
解析：
解：设□里的数为x。
漏抄括号后算式为：54÷9×75+x=498
计算得：6×75+x=498
450+x=498
x=498-450
x=48
正确算式为：54÷9×(75+48)
=6×123
=738
738
漏抄括号后算式为：54÷9×75+x=498
计算得：6×75+x=498
450+x=498
x=498-450
x=48
正确算式为：54÷9×(75+48)
=6×123
=738
738
(2)(连云港赣榆区)如图,桌子上叠放了若干本相同的书,每本书的厚度是(
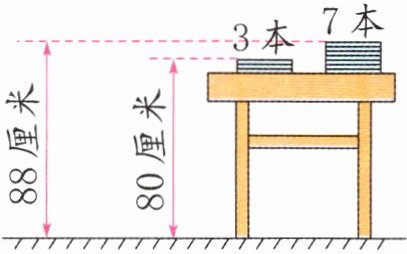
2
)厘米,桌子高(74
)厘米。答案：2 74 解析:每本书的厚度为$(88 - 80)÷(7 - 3)=2$(厘米),桌子高$80 - 3×2 = 74$(厘米)。
解析：
每本书的厚度：$(88-80)÷(7-3)=8÷4=2$（厘米）
桌子高：$80-3×2=80-6=74$（厘米）
答案：2；74
桌子高：$80-3×2=80-6=74$（厘米）
答案：2；74
(3)(扬州江都区)两个小组进行跳绳比赛,甲组6人,乙组5人。1分钟内每名同学跳绳下数记录如下表。(
| |1号|2号|3号|4号|5号|6号|
|甲组|96下|92下|88下|94下|101下|81下|
|乙组|95下|96下|87下|93下|94下| |
乙
)组同学跳绳的整体水平高,理由是(甲组平均每人跳绳的下数比乙组平均每人跳绳的下数少
)。| |1号|2号|3号|4号|5号|6号|
|甲组|96下|92下|88下|94下|101下|81下|
|乙组|95下|96下|87下|93下|94下| |
答案：乙 甲组平均每人跳绳的下数比乙组平均每人跳绳的下数少
解析：
解：甲组平均成绩：
$\begin{aligned}&(96 + 92 + 88 + 94 + 101 + 81)÷6\\=&(188 + 88 + 94 + 101 + 81)÷6\\=&(276 + 94 + 101 + 81)÷6\\=&(370 + 101 + 81)÷6\\=&(471 + 81)÷6\\=&552÷6\\=&92(\text{下})\end{aligned}$
乙组平均成绩：
$\begin{aligned}&(95 + 96 + 87 + 93 + 94)÷5\\=&(191 + 87 + 93 + 94)÷5\\=&(278 + 93 + 94)÷5\\=&(371 + 94)÷5\\=&465÷5\\=&93(\text{下})\end{aligned}$
因为$92 ＜ 93$，所以乙组同学跳绳的整体水平高，理由是甲组平均每人跳绳的下数比乙组平均每人跳绳的下数少。
乙 甲组平均每人跳绳的下数比乙组平均每人跳绳的下数少
$\begin{aligned}&(96 + 92 + 88 + 94 + 101 + 81)÷6\\=&(188 + 88 + 94 + 101 + 81)÷6\\=&(276 + 94 + 101 + 81)÷6\\=&(370 + 101 + 81)÷6\\=&(471 + 81)÷6\\=&552÷6\\=&92(\text{下})\end{aligned}$
乙组平均成绩：
$\begin{aligned}&(95 + 96 + 87 + 93 + 94)÷5\\=&(191 + 87 + 93 + 94)÷5\\=&(278 + 93 + 94)÷5\\=&(371 + 94)÷5\\=&465÷5\\=&93(\text{下})\end{aligned}$
因为$92 ＜ 93$，所以乙组同学跳绳的整体水平高，理由是甲组平均每人跳绳的下数比乙组平均每人跳绳的下数少。
乙 甲组平均每人跳绳的下数比乙组平均每人跳绳的下数少
(4)(厦门集美区)如图所示为一张长方形纸折叠后的图形,$∠2= 50^{\circ }$,则$∠1=$
80
°。答案：80
解析：
解：由折叠性质可知，∠2与折叠前的对应角相等，均为50°。
因为长方形的对边平行，所以∠1与两个∠2的和互补（平角为180°）。
则∠1 = 180° - 2×∠2 = 180° - 2×50° = 80°。
80
因为长方形的对边平行，所以∠1与两个∠2的和互补（平角为180°）。
则∠1 = 180° - 2×∠2 = 180° - 2×50° = 80°。
80
(1)(成都金牛区)有 10 人接受了市场调查:在过去的一个月里,你去了超市多少次? 调查结果如下(单位:次):3、4、2、2、2、3、1、5、3、4。下面点子图中正确表示了这个调查结果的是(
C
)。答案：C
解析：
1出现1次，2出现3次，3出现3次，4出现2次，5出现1次。
C
C
(2)(南通海门区)一只老虎追赶一只狐狸,狐狸掉到河里的点 A 处。狐狸想要尽快上岸,还不被老虎抓住,聪明的狐狸会选择
A.AB
B.AC
C.AD
C
这条路线。A.AB
B.AC
C.AD
答案：C
解析：
解：根据“直线外一点到直线的所有连线中，垂线段最短”，狐狸在点A处，要尽快上岸，需选择到河岸的垂线段。观察图形，AD是点A到下方河岸的垂线段，AC是点A到下方河岸的斜线段，AB是点A到上方河岸的垂线段但老虎在上方河岸。因狐狸要尽快上岸且不被老虎抓住，应选择下方河岸的垂线段AD。
答案：C
答案：C
(3)(淮安洪泽区)晓轩从袋子中摸球(每次摸1个球,摸完后放回搅匀),下面的说法中,正确的是(
A.若他第一次摸的是白球,则第二次一定会摸到灰球
B.若他摸了 40 次,则一定摸了 20 次灰球、20 次白球
C.若他摸了 100 次,则不可能摸了 50 次白球、50 次灰球
D.若他摸了 1000 次,则可能摸了 501 次白球、499 次灰球
D
)。A.若他第一次摸的是白球,则第二次一定会摸到灰球
B.若他摸了 40 次,则一定摸了 20 次灰球、20 次白球
C.若他摸了 100 次,则不可能摸了 50 次白球、50 次灰球
D.若他摸了 1000 次,则可能摸了 501 次白球、499 次灰球
答案：D
解析：
袋子中有2个灰球和2个白球，共4个球，每次摸球后放回搅匀，摸到灰球和白球的可能性均为$\frac{1}{2}$。
A. 每次摸球相互独立，第一次摸白球后，第二次仍可能摸到白球或灰球，A错误。
B. 摸40次是随机事件，不一定各摸20次，B错误。
C. 摸100次可能摸到50次白球和50次灰球，C错误。
D. 摸1000次，摸到501次白球和499次灰球是可能的，D正确。
答案：D
A. 每次摸球相互独立，第一次摸白球后，第二次仍可能摸到白球或灰球，A错误。
B. 摸40次是随机事件，不一定各摸20次，B错误。
C. 摸100次可能摸到50次白球和50次灰球，C错误。
D. 摸1000次，摸到501次白球和499次灰球是可能的，D正确。
答案：D
3.(盐城盐都区)运动会跳远比赛时,每名运动员都有三次试跳机会,以最好的一次成绩作为最终成绩。阳阳在跳远比赛中,第一次犯规,后两次分别跳到了图中的位置。
(1)画一画,用线段分别表示阳阳两次跳远的距离。
(2)这两条线段互相( )。(填“垂直”或“平行”)
(3)阳阳两次的成绩分别为 220 厘米和 196 厘米,康康的成绩分别为 215 厘米、205 厘米和 210 厘米。他们谁会获胜? 请说明理由。
(1)画一画,用线段分别表示阳阳两次跳远的距离。
(2)这两条线段互相( )。(填“垂直”或“平行”)
(3)阳阳两次的成绩分别为 220 厘米和 196 厘米,康康的成绩分别为 215 厘米、205 厘米和 210 厘米。他们谁会获胜? 请说明理由。
答案：
(1)
(2) 平行 (3) 阳阳 理由:以最好的成绩作为最终成绩,所以阳阳的最终成绩为 220 厘米,康康的最终成绩为 215 厘米,$220 ＞ 215$,阳阳获胜。
(1)
(2) 平行 (3) 阳阳 理由:以最好的成绩作为最终成绩,所以阳阳的最终成绩为 220 厘米,康康的最终成绩为 215 厘米,$220 ＞ 215$,阳阳获胜。