1. (南京真题)6个女孩和1个男孩玩“捉迷藏”游戏,如果男孩蒙上眼睛,他
不可能
捉到男孩;如果一个女孩蒙上眼睛,她可能
捉到男孩。(填“一定”“可能”或“不可能”)答案:不可能 可能
2. 一个布袋中装有3个白球和4个红球,这些球除了颜色其余均相同。
(1)从中任意摸出1个球,摸到(
(2)如果要使摸到白球的可能性大,那么至少还要往布袋中放入(
(1)从中任意摸出1个球,摸到(
红
)球的可能性大,摸到(白
)球的可能性小。(2)如果要使摸到白球的可能性大,那么至少还要往布袋中放入(
2
)个白球。答案:(1) 红 白 (2) 2
3. 在一个盒子里装有红球、黄球和白球各1个,从中任意摸出两个球,有
3
种可能的结果,请分别写出这几种结果:红球和黄球,红球和白球,黄球和白球
。答案:3 红球和黄球,红球和白球,黄球和白球
4. 新情境 学科融合 我们经常使用一些成语来形容事情发生的可能性大小。有以下成语:① 十拿九稳;② 平分秋色;③ 百发百中;④ 天方夜谭。按可能性从大到小的顺序将上面的成语排序:(
③①②④
)。(填序号)答案:③①②④
5. 盒子里有红球、白球和黄球共10个(除颜色外其余均相同),任意摸出一个球,若保证摸到红球的可能性最大,则红球至少有(
5
)个;若每种颜色的球都不少于2个,一次任意摸出2个球,则这2个球的颜色搭配有(6
)种。答案:5 6 解析:任意摸出一个球,若保证摸到红球的可能性最大,则红球的个数应是三种球中最多的。当红球是 5 个时,其他两种球的个数一定比红球少。如果每种颜色的球都不少于 2 个,一次任意摸出 2 个球,可能 2 个球的颜色相同,也可能不同,即红红、红白、红黄、白白、白黄、黄黄,共 6 种。
解析:
5. 4;6
解:
(1)要保证摸到红球可能性最大,红球数量需多于白球和黄球。总球数10个,当红球4个时,剩余6个分给白、黄球,最多一种颜色3个,红球数量最多,故红球至少4个。
(2)每种颜色球不少于2个,摸2个球的颜色搭配:
同色:红红、白白、黄黄(3种);
不同色:红白、红黄、白黄(3种);
共3+3=6种。
解:
(1)要保证摸到红球可能性最大,红球数量需多于白球和黄球。总球数10个,当红球4个时,剩余6个分给白、黄球,最多一种颜色3个,红球数量最多,故红球至少4个。
(2)每种颜色球不少于2个,摸2个球的颜色搭配:
同色:红红、白白、黄黄(3种);
不同色:红白、红黄、白黄(3种);
共3+3=6种。
6. 在一个不透明的袋子里装着大小完全相同的4个黄色乒乓球和3个白色乒乓球。从中任意摸一个,摸后不放回,至少摸出(
5
)个球就一定会摸到白色乒乓球。答案:5 解析:从最坏的情况开始想,有可能前 4 次都摸到黄色乒乓球,那么第 5 次肯定会摸到白色乒乓球。
解析:
5
解析:考虑最坏情况,前4次均摸到黄色乒乓球,此时袋子中仅剩白色乒乓球,故第5次一定摸到白色乒乓球。
解析:考虑最坏情况,前4次均摸到黄色乒乓球,此时袋子中仅剩白色乒乓球,故第5次一定摸到白色乒乓球。
1. 聪聪和明明轮流掷飞镖,约定掷到白色部分聪聪赢1分,掷到灰色部分明明赢1分,用下面的(
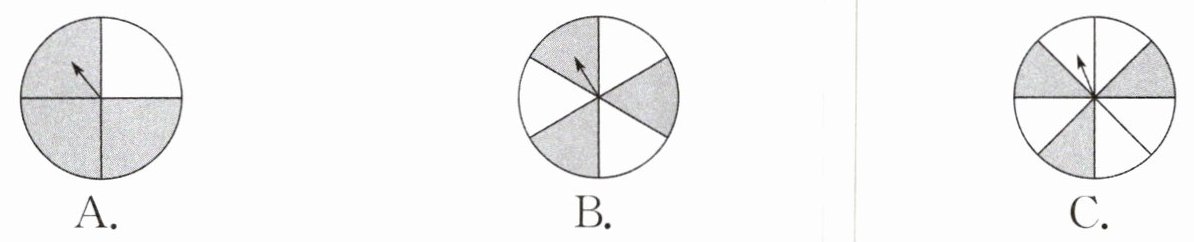
B
)镖盘公平。
答案:B