7. (2024秋·桃城区期中)两条相交直线与另一条直线在同一平面内,它们的交点个数是 (
A.1
B.2
C.3或2
D.1或2或3
D
)A.1
B.2
C.3或2
D.1或2或3
答案:D
解析:
情况1:第三条直线过两条相交直线的交点,此时交点个数为1;
情况2:第三条直线与两条相交直线中的一条平行,与另一条相交,此时交点个数为2;
情况3:第三条直线与两条相交直线都相交且不过它们的交点,此时交点个数为3;
综上,交点个数是1或2或3。
D
情况2:第三条直线与两条相交直线中的一条平行,与另一条相交,此时交点个数为2;
情况3:第三条直线与两条相交直线都相交且不过它们的交点,此时交点个数为3;
综上,交点个数是1或2或3。
D
8. 如图.(1)点B在直线AD
(2)点C在直线AD
(3)经过点C的直线共有
上
,点E在直线DC和AF
上;(2)点C在直线AD
外
,点F是直线AE
和BC
的交点;(3)经过点C的直线共有
3
条,它们分别是直线AC,BC,DC
.答案:(1)上 DC和AF (2)外 AE BC
(3)3 直线AC,BC,DC
(3)3 直线AC,BC,DC
9. 一列火车往返于A,B两个城市,中途经过C,D,E,F4个站点(共6个站点),不同的车站往返需要不同的车票.
(1)共有多少种不同的车票?
(2)一列火车往返甲、乙两个城市,如果共有n(n≥3)个站点(包括甲、乙两个城市的站点),那么有多少种不同的车票?
(1)共有多少种不同的车票?
(2)一列火车往返甲、乙两个城市,如果共有n(n≥3)个站点(包括甲、乙两个城市的站点),那么有多少种不同的车票?
答案:解:(1)两站之间的往返车票各一种,即两种,则6个站点的车票共有6×5=30(种).
(2)n个站点需要n(n−1)种不同的车票.
(2)n个站点需要n(n−1)种不同的车票.
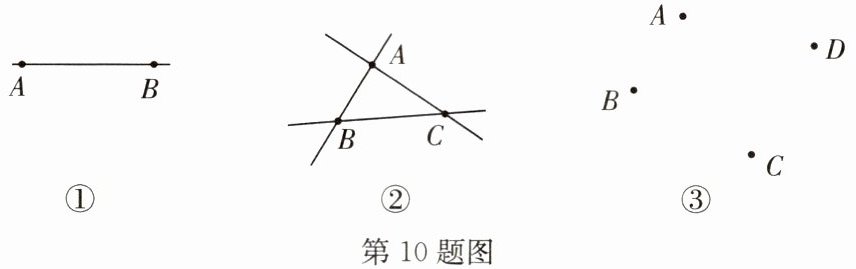
10. (1)实验观察:观察图①,由点A和点B可确定______条直线;观察图②,由不在同一直线上的三点A,B,C最多能确定______条直线;动手画一画图③中经过A,B,C,D四点中任意两点的所有直线,最多可画______条直线.
(2)探索归纳:在同一平面内,任意五个点最多能确定______条直线,任意n(n≥2)个点最多能确定______条直线.
(3)解决问题:某班40名同学在毕业后的一次聚会中,若每两人握一次手问好,那么共握______次手.
(2)探索归纳:在同一平面内,任意五个点最多能确定______条直线,任意n(n≥2)个点最多能确定______条直线.
(3)解决问题:某班40名同学在毕业后的一次聚会中,若每两人握一次手问好,那么共握______次手.

答案:
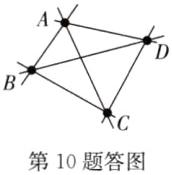
(1)1 3 6 画一画如答图所示.
(2)10 $\frac{n(n−1)}{2}$ (3)780
(1)1 3 6 画一画如答图所示.

(2)10 $\frac{n(n−1)}{2}$ (3)780