9. (10分)如图,在同一平面内有四个点A,B,C,D,请按要求完成下列问题。(不要求写出作法和结论)
(1)作射线AC;
(2)作直线BD与射线AC相交于点O;
(3)分别作线段AB,AD;
(4)我们容易判断出线段$AB+AD$与BD的数量关系是______,理由是______。

(1)作射线AC;
(2)作直线BD与射线AC相交于点O;
(3)分别作线段AB,AD;
(4)我们容易判断出线段$AB+AD$与BD的数量关系是______,理由是______。

答案:
解:(1)(2)(3)如答图所示.
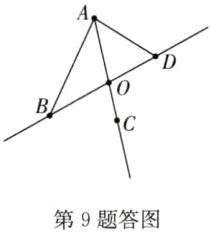
(4)AB+AD>BD 两点之间,线段最短
解:(1)(2)(3)如答图所示.

(4)AB+AD>BD 两点之间,线段最短
10. (10分)如图,已知A,B,C,D四点在同一直线上,点D在线段AB上,C是线段AB的中点。
(1)若线段$AB= 18$,$BD= 2CD$,求线段AD的长度;
(2)若$AD:BD= 3:2$,且$CD= 2$,求线段AB的长度。

(1)若线段$AB= 18$,$BD= 2CD$,求线段AD的长度;
(2)若$AD:BD= 3:2$,且$CD= 2$,求线段AB的长度。

答案:解:(1)因为线段AB=18,C是线段AB的中点,
所以AC=BC=$\frac{1}{2}$AB=9.
因为BD=2CD,
所以CD=$\frac{1}{3}$BC=$\frac{1}{3}×9$=3,
所以AD=AC+CD=9+3=12.
(2)因为AD:BD=3:2,
所以设AD=3x,BD=2x,
所以AB=5x,
所以AC=AD-CD=3x-2,BC=BD+CD=2x+2.
因为C是线段AB的中点,
所以AC=BC,
所以3x-2=2x+2,解得x=4,
所以AB=5×4=20.
所以AC=BC=$\frac{1}{2}$AB=9.
因为BD=2CD,
所以CD=$\frac{1}{3}$BC=$\frac{1}{3}×9$=3,
所以AD=AC+CD=9+3=12.
(2)因为AD:BD=3:2,
所以设AD=3x,BD=2x,
所以AB=5x,
所以AC=AD-CD=3x-2,BC=BD+CD=2x+2.
因为C是线段AB的中点,
所以AC=BC,
所以3x-2=2x+2,解得x=4,
所以AB=5×4=20.
11. (14分)如图①,将一张长为60cm,宽为40cm的长方形纸片,在四个角上分别剪去边长为xcm的小正方形,将剩下部分折成如图②所示的一个无盖长方体盒子。
(1)若$x= 5$,则将剩下部分折成的无盖长方体盒子的体积为
(2)若将剩下部分折成的无盖长方体盒子的底面的长是宽的2倍,求该盒子的体积。

解:由题意知,无盖长方体盒子的长为(60-2x)cm,宽为(40-2x)cm,则
60-2x=2(40-2x),解得x=10,
所以60-2x=40,40-2x=20.
40×20×10=8000(cm³).
答:该盒子的体积为8000cm³.
(1)若$x= 5$,则将剩下部分折成的无盖长方体盒子的体积为
7500
$cm^{3}$;(2)若将剩下部分折成的无盖长方体盒子的底面的长是宽的2倍,求该盒子的体积。

解:由题意知,无盖长方体盒子的长为(60-2x)cm,宽为(40-2x)cm,则
60-2x=2(40-2x),解得x=10,
所以60-2x=40,40-2x=20.
40×20×10=8000(cm³).
答:该盒子的体积为8000cm³.
答案:(1)7500
(2)解:由题意知,无盖长方体盒子的长为(60-2x)cm,宽为(40-2x)cm,则
60-2x=2(40-2x),解得x=10,
所以60-2x=40,40-2x=20.
40×20×10=8000(cm³).
答:该盒子的体积为8000cm³.
(2)解:由题意知,无盖长方体盒子的长为(60-2x)cm,宽为(40-2x)cm,则
60-2x=2(40-2x),解得x=10,
所以60-2x=40,40-2x=20.
40×20×10=8000(cm³).
答:该盒子的体积为8000cm³.
12. (14分)如图,点A,O,B在同一条直线上,射线OD平分$∠BOC$,设$∠AOD= α(135^{\circ }<α<180^{\circ })$。
(1)当$α=150^{\circ }$时,求$∠AOC$的度数;
(2)若在$∠AOD$的内部画射线OE,使$∠BOE= 90^{\circ }$,求证:$∠DOE与∠DOC$互余;
(3)画射线OE,若$∠DOE与∠DOC$互余,求$∠BOE$的度数。(用含α的代数式表示)

(1)当$α=150^{\circ }$时,求$∠AOC$的度数;
(2)若在$∠AOD$的内部画射线OE,使$∠BOE= 90^{\circ }$,求证:$∠DOE与∠DOC$互余;
(3)画射线OE,若$∠DOE与∠DOC$互余,求$∠BOE$的度数。(用含α的代数式表示)

答案:
(1)解:因为∠AOD=α=150°,
所以∠BOD=180°-∠AOD=30°.
因为OD平分∠BOC,
所以∠DOC=∠BOD=30°,
所以∠AOC=∠AOD-∠DOC=150°-30°=120°.
(2)证明:因为在∠AOD的内部画射线OE,∠BOE=90°,所以∠BOD+∠DOE=90°.
因为OD平分∠BOC,
所以∠DOC=∠BOD,
所以∠DOC+∠DOE=90°,
所以∠DOE与∠DOC互余.
(3)解:当射线OE在∠AOD的内部时,如答图①.

因为OD平分∠BOC,所以∠DOC=∠BOD.
因为∠DOE+∠DOC=90°,
所以∠DOE+∠BOD=90°,所以∠BOE=90°.
当射线OE在∠AOD的外部时,如答图②.
因为∠AOD=α,所以∠BOD=180°-α.
因为射线OD平分∠BOC,
所以∠BOC=2∠BOD=2(180°-α).
因为∠DOE+∠DOC=90°,即∠EOC=90°,
所以∠BOE=90°-2(180°-α)=2α-270°.
所以∠BOE=90°或∠BOE=2α-270°.
(1)解:因为∠AOD=α=150°,
所以∠BOD=180°-∠AOD=30°.
因为OD平分∠BOC,
所以∠DOC=∠BOD=30°,
所以∠AOC=∠AOD-∠DOC=150°-30°=120°.
(2)证明:因为在∠AOD的内部画射线OE,∠BOE=90°,所以∠BOD+∠DOE=90°.
因为OD平分∠BOC,
所以∠DOC=∠BOD,
所以∠DOC+∠DOE=90°,
所以∠DOE与∠DOC互余.
(3)解:当射线OE在∠AOD的内部时,如答图①.

因为OD平分∠BOC,所以∠DOC=∠BOD.
因为∠DOE+∠DOC=90°,
所以∠DOE+∠BOD=90°,所以∠BOE=90°.
当射线OE在∠AOD的外部时,如答图②.
因为∠AOD=α,所以∠BOD=180°-α.
因为射线OD平分∠BOC,
所以∠BOC=2∠BOD=2(180°-α).
因为∠DOE+∠DOC=90°,即∠EOC=90°,
所以∠BOE=90°-2(180°-α)=2α-270°.
所以∠BOE=90°或∠BOE=2α-270°.