1.(2024秋·闵行区期中)下列各式中,不是代数式的是(
A.$ vt $
B.5
C.$ \frac{2 - x}{6} $
D.$ 2x + y = 1 $
D
)A.$ vt $
B.5
C.$ \frac{2 - x}{6} $
D.$ 2x + y = 1 $
答案:D
2. 无论$ a $取何值,下列代数式的值一定是正数的是(
A.$ a + 2 $
B.$ |a + 2| $
C.$ a^{2} + 2 $
D.$ -a^{2} + 2 $
C
)A.$ a + 2 $
B.$ |a + 2| $
C.$ a^{2} + 2 $
D.$ -a^{2} + 2 $
答案:C
解析:
A. 当$a=-3$时,$a + 2=-1$,不是正数;
B. 当$a=-2$时,$|a + 2|=0$,不是正数;
C. 因为$a^{2}\geq0$,所以$a^{2} + 2\geq2$,一定是正数;
D. 当$a=2$时,$-a^{2} + 2=-2$,不是正数。
C
B. 当$a=-2$时,$|a + 2|=0$,不是正数;
C. 因为$a^{2}\geq0$,所以$a^{2} + 2\geq2$,一定是正数;
D. 当$a=2$时,$-a^{2} + 2=-2$,不是正数。
C
3. 某产品的成本为$ a $元,按成本加价四成作为定价销售,因季节原因按定价的六折出售,降价后的售价为(
A.$ (60\% - 40\%)a $元
B.$ 60\% × 40\%a $元
C.$ (1 + 40\%) × 60\%a $元
D.$ (1 + 40\%)(1 - 60\%)a $元
C
)A.$ (60\% - 40\%)a $元
B.$ 60\% × 40\%a $元
C.$ (1 + 40\%) × 60\%a $元
D.$ (1 + 40\%)(1 - 60\%)a $元
答案:C
解析:
成本为$a$元,加价四成后的定价为$(1 + 40\%)a$元,按定价的六折出售,降价后的售价为$(1 + 40\%)×60\%a$元。
C
C
4.(2024秋·镇江月考)把有理数$ a 代入 |a + 4| - 10 得到 a_{1} $,称为第一次操作;再将$ a_{1} 作为 a 的值代入得到 a_{2} $,称为第二次操作;….若$ a = -12 $,经过第2024次操作后得到的结果是(
A.-2
B.-6
C.-8
D.-10
C
)A.-2
B.-6
C.-8
D.-10
答案:C
解析:
当$a=-12$时,
第一次操作:$a_{1}=|-12 + 4| - 10=|-8| - 10=8 - 10=-2$;
第二次操作:$a_{2}=|-2 + 4| - 10=|2| - 10=2 - 10=-8$;
第三次操作:$a_{3}=|-8 + 4| - 10=|-4| - 10=4 - 10=-6$;
第四次操作:$a_{4}=|-6 + 4| - 10=|-2| - 10=2 - 10=-8$;
第五次操作:$a_{5}=|-8 + 4| - 10=4 - 10=-6$;
……
从第二次操作开始,结果以$-8$,$-6$循环,循环节长度为$2$。
$(2024 - 1)÷2=2023÷2=1011\cdots\cdots1$,余数为$1$,对应循环节第一个数$-8$。
C
第一次操作:$a_{1}=|-12 + 4| - 10=|-8| - 10=8 - 10=-2$;
第二次操作:$a_{2}=|-2 + 4| - 10=|2| - 10=2 - 10=-8$;
第三次操作:$a_{3}=|-8 + 4| - 10=|-4| - 10=4 - 10=-6$;
第四次操作:$a_{4}=|-6 + 4| - 10=|-2| - 10=2 - 10=-8$;
第五次操作:$a_{5}=|-8 + 4| - 10=4 - 10=-6$;
……
从第二次操作开始,结果以$-8$,$-6$循环,循环节长度为$2$。
$(2024 - 1)÷2=2023÷2=1011\cdots\cdots1$,余数为$1$,对应循环节第一个数$-8$。
C
5.(2024秋·盐城期中)“$ a $的2倍与5的和”用代数式表示是
2a+5
.答案:2a+5
6. 如图,阴影部分的面积用含$ x $的式子可表示为
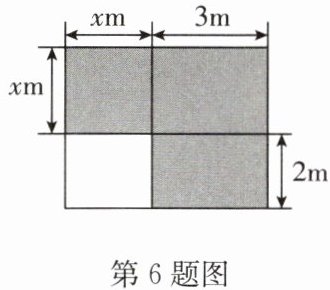
x²+3x+6
$ m^{2} $.
答案:x²+3x+6
解析:
$x^{2}+3x+6$
7. 如图,若开始输入的$ x 的值为 \frac{3}{4} $,按此程序运算,最后输出的结果为
13
.答案:13
解析:
第一次运算:$2×\frac{3}{4}+1=\frac{3}{2}+1=\frac{5}{2}$,$\frac{5}{2}<10$;
第二次运算:$2×\frac{5}{2}+1=5+1=6$,$6<10$;
第三次运算:$2×6+1=12+1=13$,$13>10$,输出结果。
13
第二次运算:$2×\frac{5}{2}+1=5+1=6$,$6<10$;
第三次运算:$2×6+1=12+1=13$,$13>10$,输出结果。
13
8. 已知$ (2x - 1)^{5} = a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + a_{4}x^{4} + a_{5}x^{5} $.
(1)当$ x = 0 $时,$ a_{0} = $
(2)$ a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = $
(1)当$ x = 0 $时,$ a_{0} = $
-1
;(2)$ a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = $
2
.答案:(1)-1 (2)2
解析:
(1)当$x = 0$时,$(2×0 - 1)^{5}=a_{0}+a_{1}×0 + a_{2}×0^{2}+a_{3}×0^{3}+a_{4}×0^{4}+a_{5}×0^{5}$,即$(-1)^{5}=a_{0}$,所以$a_{0}=-1$。
(2)当$x = 1$时,$(2×1 - 1)^{5}=a_{0}+a_{1}×1 + a_{2}×1^{2}+a_{3}×1^{3}+a_{4}×1^{4}+a_{5}×1^{5}$,即$1^{5}=a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$,所以$a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=1$。又因为$a_{0}=-1$,所以$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=1 - a_{0}=1 - (-1)=2$。
(1)-1 (2)2
(2)当$x = 1$时,$(2×1 - 1)^{5}=a_{0}+a_{1}×1 + a_{2}×1^{2}+a_{3}×1^{3}+a_{4}×1^{4}+a_{5}×1^{5}$,即$1^{5}=a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$,所以$a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=1$。又因为$a_{0}=-1$,所以$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=1 - a_{0}=1 - (-1)=2$。
(1)-1 (2)2