2. (2024 秋·广陵区期中)如图,用三角形和六边形按如图所示的规律拼图案.
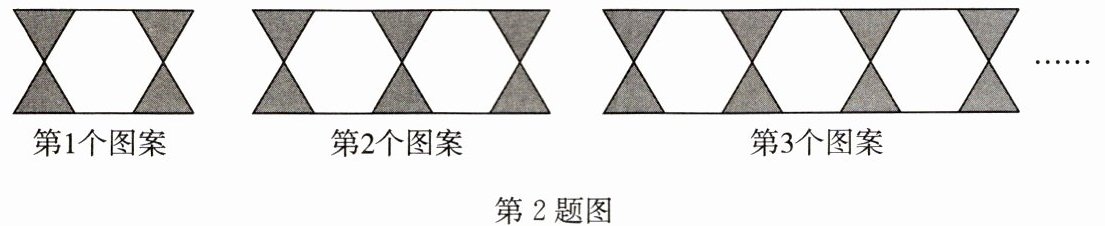
(1)第 3 个图案中,三角形有
(2)第 5 个图案中,三角形有
(3)第 $ n $($ n $ 为正整数)个图案中,三角形有
(4)是否存在某个符合上述规律的图案,其中有 100 个三角形和 50 个六边形?如果存在,指出是第几个图案;如果不存在,请说明理由.
解:不存在.理由如下:
令2n+2=100,解得n=49,
即第49个图案中,三角形的个数为100.
又第50个图案中有50个六边形,且49≠50,
所以不存在某个符合上述规律的图案,其中有100个三角形和50个六边形.

(1)第 3 个图案中,三角形有
8
个,六边形有3
个;(2)第 5 个图案中,三角形有
12
个,六边形有5
个;(3)第 $ n $($ n $ 为正整数)个图案中,三角形有
2n+2
个,六边形有n
个;(4)是否存在某个符合上述规律的图案,其中有 100 个三角形和 50 个六边形?如果存在,指出是第几个图案;如果不存在,请说明理由.
解:不存在.理由如下:
令2n+2=100,解得n=49,
即第49个图案中,三角形的个数为100.
又第50个图案中有50个六边形,且49≠50,
所以不存在某个符合上述规律的图案,其中有100个三角形和50个六边形.
答案:2.(1)8 3
(2)12 5
(3)2n+2 n
(4)解:不存在.理由如下:
令2n+2=100,解得n=49,
即第49个图案中,三角形的个数为100.
又第50个图案中有50个六边形,且49≠50,
所以不存在某个符合上述规律的图案,其中有100个三角形和50个六边形.
(2)12 5
(3)2n+2 n
(4)解:不存在.理由如下:
令2n+2=100,解得n=49,
即第49个图案中,三角形的个数为100.
又第50个图案中有50个六边形,且49≠50,
所以不存在某个符合上述规律的图案,其中有100个三角形和50个六边形.