9. 有理数a,b,c,d在数轴上对应点的位置如图所示,其中有一对互为相反数,它们是 (
A.a与d
B.b与d
C.c与d
D.a与c
C
)A.a与d
B.b与d
C.c与d
D.a与c
答案：C
10. (2024秋·襄都区月考)在数轴上,若点A,B分别表示互为相反数的两个数,并且这两个点的距离是7,点A在原点的左侧,则点A表示的数为
−3.5
.答案：−3.5
解析：
设点A表示的数为$x$，因为点A，B互为相反数，所以点B表示的数为$-x$。
由于点A在原点左侧，所以$x＜0$，点B在原点右侧，$-x＞0$。
两点距离为7，可得$-x - x = 7$，即$-2x = 7$，解得$x=-\frac{7}{2}=-3.5$。
$-3.5$
由于点A在原点左侧，所以$x＜0$，点B在原点右侧，$-x＞0$。
两点距离为7，可得$-x - x = 7$，即$-2x = 7$，解得$x=-\frac{7}{2}=-3.5$。
$-3.5$
11. (1)化简下列各式:①-(-2);②+(-$\frac{1}{5}$);③-[-(-4)];④-[-(+3.5)];⑤-{-[-(-5)]};⑥-{-[-(+5)]};
(2)若+5前面有2026个负号,则化简后的结果是多少?若-5前面有2025个负号,则化简后的结果是多少?你能总结出什么规律?
(2)若+5前面有2026个负号,则化简后的结果是多少?若-5前面有2025个负号,则化简后的结果是多少?你能总结出什么规律?
答案：解:(1)①−(−2)=2;②+(−$\frac{1}{5}$)=−$\frac{1}{5}$;③−[−(−4)]=−4;④−[−(+3.5)]=3.5;⑤−{−[−(−5)]}=5;⑥−{−[−(+5)]}=−5. (2)化简后的结果是+5;化简后的结果是+5.总结规律:一个数的前面有奇数个负号，化简的结果等于它的相反数;有偶数个负号，化简的结果等于它本身.
12. 如图,已知A,B,C,D四个点在一条没有标明原点的数轴上.
(1)若点A和点C表示的数互为相反数,则原点为______;
(2)若点B和点D表示的数互为相反数,则原点为______;
(3)若点A和点D表示的数互为相反数,请在数轴上标出原点的位置.
(1)若点A和点C表示的数互为相反数,则原点为______;
(2)若点B和点D表示的数互为相反数,则原点为______;
(3)若点A和点D表示的数互为相反数,请在数轴上标出原点的位置.
答案：
(1)B (2)C (3)解:如答图所示.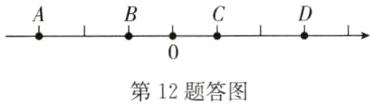
(1)B (2)C (3)解:如答图所示.
13. 已知表示数a的点在数轴上的位置如图所示.
(1)在数轴上标出表示数a的相反数的点的位置;
(2)若表示数a的点与表示其相反数的点相距20个单位长度,则a是多少?
(3)在(2)的条件下,若表示数b的点与表示数a的相反数的点相距5个单位长度,求数b的值.
(1)在数轴上标出表示数a的相反数的点的位置;
(2)若表示数a的点与表示其相反数的点相距20个单位长度,则a是多少?
(3)在(2)的条件下,若表示数b的点与表示数a的相反数的点相距5个单位长度,求数b的值.
答案：
解:(1)如答图所示.
(2)由题意得a=−10.(3)由(2)可得−a=10,当表示数b的点在表示数−a的点的右边时， b=10+5=15;当表示数b的点在表示数−a的点的左边时，b=10−5=5.故b的值是5或15.
解:(1)如答图所示.
(2)由题意得a=−10.(3)由(2)可得−a=10,当表示数b的点在表示数−a的点的右边时， b=10+5=15;当表示数b的点在表示数−a的点的左边时，b=10−5=5.故b的值是5或15.