24. (8分)下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,文艺小组每次活动时间比科技小组每次活动时间多$0.5$小时.设文艺小组每次活动时间为$x$小时,请根据表中信息完成下列问题.
| | 课外兴趣小组活动总时间/时 | 文艺小组活动次数 | 科技小组活动次数 |
| 七年级 | $12.5$ | $4$ | $3$ |
| 八年级 | $10.5$ | $3$ | $a$ |
| 九年级 | $9.5$ | $m$ | $n$ |
(1)科技小组每次活动时间为多长时间?
(2)求八年级科技小组活动次数$a$的值;
(3)求$m + n$的值.
| | 课外兴趣小组活动总时间/时 | 文艺小组活动次数 | 科技小组活动次数 |
| 七年级 | $12.5$ | $4$ | $3$ |
| 八年级 | $10.5$ | $3$ | $a$ |
| 九年级 | $9.5$ | $m$ | $n$ |
(1)科技小组每次活动时间为多长时间?
(2)求八年级科技小组活动次数$a$的值;
(3)求$m + n$的值.
答案:(1)依题意得$4x + 3(x - 0.5)=12.5$,解得$x=2$,故$2 - 0.5=1.5$(时),答:科技小组每次活动时间为1.5小时;(2)根据题意得$3×2 + 1.5a=10.5$,解得$a=3$,$\therefore a$的值为3;(3)$\because$九年级课外兴趣小组活动总时间为9.5小时,$\therefore 2m + 1.5n=9.5$,$\because m$与$n$是自然数,$\therefore m=1$,$n=5$或$m=4$,$n=1$,$\therefore m + n=6$或$m + n=5$
解析:
(1) 设文艺小组每次活动时间为$x$小时,因为文艺小组每次活动时间比科技小组多$0.5$小时,所以科技小组每次活动时间为$(x - 0.5)$小时。
根据七年级数据:$4x + 3(x - 0.5) = 12.5$,
解得$x = 2$,则科技小组每次活动时间为$2 - 0.5 = 1.5$小时。
答:科技小组每次活动时间为$1.5$小时。
(2) 由(1)知文艺小组每次$2$小时,科技小组每次$1.5$小时。
根据八年级数据:$3×2 + 1.5a = 10.5$,
解得$a = 3$。
(3) 根据九年级数据:$2m + 1.5n = 9.5$,整理得$4m + 3n = 19$($m,n$为自然数)。
当$m = 1$时,$n = 5$;当$m = 4$时,$n = 1$。
故$m + n = 1 + 5 = 6$或$m + n = 4 + 1 = 5$。
综上,$m + n$的值为$5$或$6$。
根据七年级数据:$4x + 3(x - 0.5) = 12.5$,
解得$x = 2$,则科技小组每次活动时间为$2 - 0.5 = 1.5$小时。
答:科技小组每次活动时间为$1.5$小时。
(2) 由(1)知文艺小组每次$2$小时,科技小组每次$1.5$小时。
根据八年级数据:$3×2 + 1.5a = 10.5$,
解得$a = 3$。
(3) 根据九年级数据:$2m + 1.5n = 9.5$,整理得$4m + 3n = 19$($m,n$为自然数)。
当$m = 1$时,$n = 5$;当$m = 4$时,$n = 1$。
故$m + n = 1 + 5 = 6$或$m + n = 4 + 1 = 5$。
综上,$m + n$的值为$5$或$6$。
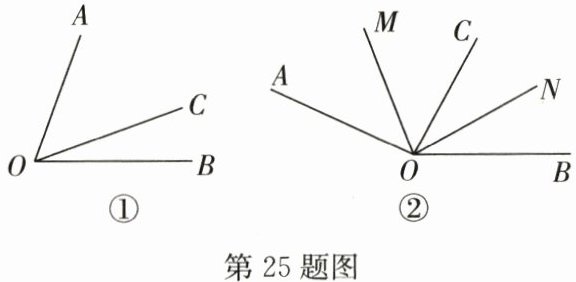
25. (10分)定义:从$\angle\alpha(45^{\circ}<\alpha<90^{\circ})$的顶点出发,在$\angle\alpha$的内部作一条射线,若该射线将$\angle\alpha$分得的两个角中有一个角与$\angle\alpha$互为余角,则称该射线为$\angle\alpha$的“分余线”.(1)如图$①,\angle AOB = 70^{\circ},\angle AOC = 50^{\circ},$请判断OC是否为$\angle AOB$的“分余线”,并说明理由;(2)若OC平分$\angle AOB,$且OC为$\angle AOB$的“分余线”,则$\angle AOB = $
$60^{\circ}$
;(3)如图$②,\angle AOB = 155^{\circ},$在$\angle AOB$的内部作射线OC,OM,ON,使OM为$\angle AOC$的平分线,ON为$\angle BOC$的“分余线”.当OC为$\angle MON$的“分余线”时,求$\angle AOC$的度数.
答案:(1)解:$OC$是$\angle AOB$的“分余线”,理由如下:$\because \angle AOB = 70^{\circ}$,$\angle AOC = 50^{\circ}$,$\therefore \angle BOC=\angle AOB - \angle AOC=70^{\circ}-50^{\circ}=20^{\circ}$,$\therefore \angle BOC+\angle AOB=20^{\circ}+70^{\circ}=90^{\circ}$,$\therefore OC$是$\angle AOB$的“分余线”;(2)$60^{\circ}$;(3)解:设$\angle AOC=2x$,$\because OM$为$\angle AOC$的平分线,$\therefore \angle COM=\frac{1}{2}\angle AOC=x$,$\because \angle AOB=155^{\circ}$,$\therefore \angle BOC=\angle AOB - \angle AOC=155^{\circ}-2x$,$\because ON$为$\angle BOC$的“分余线”,$OC$为$\angle MON$的“分余线”,分情况讨论:①$\angle BON+\angle BOC=90^{\circ}$,$\angle MOC+\angle MON=90^{\circ}$,$\therefore \angle BON=90^{\circ}-(155^{\circ}-2x)=2x - 65^{\circ}$,$\therefore \angle MON=\angle BOM - \angle BON=155^{\circ}-x-(2x - 65^{\circ})=220^{\circ}-3x$,$\therefore x + 220^{\circ}-3x=90^{\circ}$,解得$x=65^{\circ}$,此时$\angle BOC=25^{\circ}$,不符合题意,舍去;②$\angle BON+\angle BOC=90^{\circ}$,$\angle CON+\angle MON=90^{\circ}$,$\therefore \angle BON=2x - 65^{\circ}$,$\because \angle CON=\angle BOC - \angle BON=155^{\circ}-2x-(2x - 65^{\circ})=220^{\circ}-4x$,$\therefore 220^{\circ}-4x + 220^{\circ}-3x=90^{\circ}$,解得$x=50^{\circ}$,$\therefore \angle AOC=2x=50^{\circ}×2=100^{\circ}$;③$\angle CON+\angle BOC=90^{\circ}$,$\angle MOC+\angle MON=90^{\circ}$,$\therefore \angle CON=90^{\circ}-\angle BOC=90^{\circ}-(155^{\circ}-2x)=2x - 65^{\circ}$,$\therefore \angle MON=\angle MOC+\angle CON=x + 2x - 65^{\circ}=3x - 65^{\circ}$,$\therefore x + 3x - 65^{\circ}=90^{\circ}$,解得$x=38.75^{\circ}$,$\therefore \angle AOC=2x=38.75^{\circ}×2=77.5^{\circ}$;④$\angle CON+\angle BOC=90^{\circ}$,$\angle CON+\angle MON=90^{\circ}$,$\therefore \angle CON=2x - 65^{\circ}$,且$\angle MON=\angle BOC$,$\therefore \angle MOC=\angle BON$,$\because \angle BON=(155^{\circ}-2x)-(2x - 65^{\circ})=220^{\circ}-4x$,$\therefore x=220^{\circ}-4x$,解得$x=44^{\circ}$,$\therefore \angle AOC=2x=44^{\circ}×2=88^{\circ}$,综上所述,满足条件的$\angle AOC$的度数为$100^{\circ}$或$77.5^{\circ}$或$88^{\circ}$