1. (1)如图①,已知 O 为直线 AD 上一点,∠AOC 与∠AOB 互补,OM,ON 分别为∠AOC 与∠AOB 的平分线,若∠MON = $40^{\circ}$,求∠AOC 与∠AOB 的度数;
(2)如图②,∠AOB : ∠BOC = 3 : 2,OD 是∠BOC 的平分线,OE 是∠AOC 的平分线,且∠BOE = $12^{\circ}$,求∠DOE 的度数.
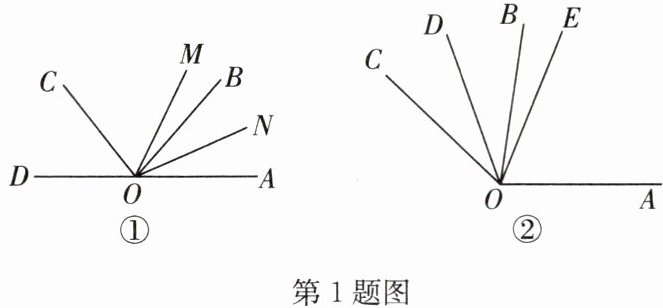
(2)如图②,∠AOB : ∠BOC = 3 : 2,OD 是∠BOC 的平分线,OE 是∠AOC 的平分线,且∠BOE = $12^{\circ}$,求∠DOE 的度数.

答案:1.解:(1)设∠AOB=x.
因为∠AOC与∠AOB互补,
所以∠AOC=180°-x.
由题意,得∠AOM-∠AON=∠MON,
即$\frac{1}{2}$(180°-x)-$\frac{1}{2}$x=40°,解得x=50°,
∴∠AOB=50°,∠AOC=130°.
(2)设∠AOB=3y,∠BOC=2y,
则∠AOC=∠AOB+∠BOC=5y.
∵OE是∠AOC的平分线,
∴∠AOE=$\frac{1}{2}$∠AOC=$\frac{5}{2}$y,
∴∠BOE=∠AOB-∠AOE=3y-$\frac{5}{2}$y=$\frac{1}{2}$y.
∵∠BOE=12°,∴$\frac{1}{2}$y=12°,解得y=24°.
∵OD是∠BOC的平分线,
∴∠BOD=$\frac{1}{2}$∠BOC=y=24°,
∴∠DOE=∠BOD+∠BOE=24°+12°=36°.
因为∠AOC与∠AOB互补,
所以∠AOC=180°-x.
由题意,得∠AOM-∠AON=∠MON,
即$\frac{1}{2}$(180°-x)-$\frac{1}{2}$x=40°,解得x=50°,
∴∠AOB=50°,∠AOC=130°.
(2)设∠AOB=3y,∠BOC=2y,
则∠AOC=∠AOB+∠BOC=5y.
∵OE是∠AOC的平分线,
∴∠AOE=$\frac{1}{2}$∠AOC=$\frac{5}{2}$y,
∴∠BOE=∠AOB-∠AOE=3y-$\frac{5}{2}$y=$\frac{1}{2}$y.
∵∠BOE=12°,∴$\frac{1}{2}$y=12°,解得y=24°.
∵OD是∠BOC的平分线,
∴∠BOD=$\frac{1}{2}$∠BOC=y=24°,
∴∠DOE=∠BOD+∠BOE=24°+12°=36°.
2. O 为直线 AB 上一点,在直线 AB 同侧任作射线 OC,OD,使得∠COD = $90^{\circ}$.
(1)如图①,过点 O 作射线 OE,使 OE 为∠AOD 的平分线,当∠COE = $25^{\circ}$时,求∠BOD 的度数;
(2)如图②,过点 O 作射线 OE,当 OE 恰好为∠AOC 的平分线时,另作射线 OF,使得 OF 平分∠BOD,求∠EOF 的度数;
(3)过点 O 作射线 OE,当 OC 恰好为∠AOE 的平分线时,另作射线 OF,使得 OF 平分∠COD,当∠EOF = $10^{\circ}$时,求∠BOD 的度数.

(1)如图①,过点 O 作射线 OE,使 OE 为∠AOD 的平分线,当∠COE = $25^{\circ}$时,求∠BOD 的度数;
(2)如图②,过点 O 作射线 OE,当 OE 恰好为∠AOC 的平分线时,另作射线 OF,使得 OF 平分∠BOD,求∠EOF 的度数;
(3)过点 O 作射线 OE,当 OC 恰好为∠AOE 的平分线时,另作射线 OF,使得 OF 平分∠COD,当∠EOF = $10^{\circ}$时,求∠BOD 的度数.

答案:
2.解:(1)∵∠COD=90°,∠COE=25°,
∴∠DOE=∠COD-∠COE=90°-25°=65°.
∵OE为∠AOD的平分线,
∴∠AOD=2∠DOE=130°,
∴∠BOD=180°-∠AOD=50°.
(2)∵∠COD=90°,
∴∠AOC+∠BOD=180°-∠COD=90°.
∵OE为∠AOC的平分线,OF平分∠BOD,
∴∠EOC=$\frac{1}{2}$∠AOC,∠DOF=$\frac{1}{2}$∠BOD,
∴∠EOF=∠COD+∠EOC+∠DOF
=90°+$\frac{1}{2}$(∠AOC+∠BOD)
=90°+$\frac{1}{2}$×90°
=135°.
(3)分两种情况:
当OF在∠EOD的内部时,如答图①.

∵∠COD=90°,OF平分∠COD,
∴∠COF=$\frac{1}{2}$∠COD=45°,
∴∠COE=∠COF-∠EOF=45°-10°=35°.
∵OC平分∠AOE,∴∠AOC=∠COE=35°,
∴∠BOD=180°-∠AOC-∠COD=180°-35°-90°=55°.
当OF在∠EOD的外部时,如答图②.

∵∠COD=90°,OF平分∠COD,
∴∠COF=$\frac{1}{2}$∠COD=45°,
∴∠COE=∠COF+∠EOF=45°+10°=55°.
∵OC平分∠AOE,∴∠AOC=∠COE=55°,
∴∠BOD=180°-∠AOC-∠COD=180°-55°-90°=35°.
综上所述,∠BOD的度数为55°或35°.
2.解:(1)∵∠COD=90°,∠COE=25°,
∴∠DOE=∠COD-∠COE=90°-25°=65°.
∵OE为∠AOD的平分线,
∴∠AOD=2∠DOE=130°,
∴∠BOD=180°-∠AOD=50°.
(2)∵∠COD=90°,
∴∠AOC+∠BOD=180°-∠COD=90°.
∵OE为∠AOC的平分线,OF平分∠BOD,
∴∠EOC=$\frac{1}{2}$∠AOC,∠DOF=$\frac{1}{2}$∠BOD,
∴∠EOF=∠COD+∠EOC+∠DOF
=90°+$\frac{1}{2}$(∠AOC+∠BOD)
=90°+$\frac{1}{2}$×90°
=135°.
(3)分两种情况:
当OF在∠EOD的内部时,如答图①.

∵∠COD=90°,OF平分∠COD,
∴∠COF=$\frac{1}{2}$∠COD=45°,
∴∠COE=∠COF-∠EOF=45°-10°=35°.
∵OC平分∠AOE,∴∠AOC=∠COE=35°,
∴∠BOD=180°-∠AOC-∠COD=180°-35°-90°=55°.
当OF在∠EOD的外部时,如答图②.

∵∠COD=90°,OF平分∠COD,
∴∠COF=$\frac{1}{2}$∠COD=45°,
∴∠COE=∠COF+∠EOF=45°+10°=55°.
∵OC平分∠AOE,∴∠AOC=∠COE=55°,
∴∠BOD=180°-∠AOC-∠COD=180°-55°-90°=35°.
综上所述,∠BOD的度数为55°或35°.