1. 如图,已知线段 $ AB = 90cm $,C 是线段 AB 上任意一点(不与点 A,B 重合)。

(1) 若 M,N 分别是 AC,BC 的中点,求 MN 的长度;
(2) 若 $ AM = \frac{1}{3}AC $,$ BN = \frac{1}{3}BC $,求 MN 的长;
(3) 在(2)的条件下,若 $ BC = 30cm $且点 G 在直线 AB 上,$ GB = 15cm $,求 MG 的长度。

(1) 若 M,N 分别是 AC,BC 的中点,求 MN 的长度;
(2) 若 $ AM = \frac{1}{3}AC $,$ BN = \frac{1}{3}BC $,求 MN 的长;
(3) 在(2)的条件下,若 $ BC = 30cm $且点 G 在直线 AB 上,$ GB = 15cm $,求 MG 的长度。
答案:1.解:(1)∵M,N分别是AC,BC的中点,
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$AB.
∵AB=90cm,
∴MN=90×$\frac{1}{2}$=45(cm).
(2)∵AM=$\frac{1}{3}$AC,BN=$\frac{1}{3}$BC,
∴MC=$\frac{2}{3}$AC,CN=$\frac{2}{3}$BC,
∴MN=MC+CN=$\frac{2}{3}$AC+$\frac{2}{3}$BC=$\frac{2}{3}$AB.
∵AB=90cm,
∴MN=$\frac{2}{3}$×90=60(cm).
(3)∵AB=90cm,BC=30cm,
∴AC=AB−BC=90−30=60(cm).
∵AM=$\frac{1}{3}$AC,
∴AM=$\frac{1}{3}$×60=20(cm),
∴MB=90−20=70(cm).
当点G在线段AB上时,
MG=MB−GB=70−15=55(cm);
当点G在线段AB的延长线上时,
MG=MB+GB=70+15=85(cm).
综上可知,MG的长度为55cm或85cm.
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$AB.
∵AB=90cm,
∴MN=90×$\frac{1}{2}$=45(cm).
(2)∵AM=$\frac{1}{3}$AC,BN=$\frac{1}{3}$BC,
∴MC=$\frac{2}{3}$AC,CN=$\frac{2}{3}$BC,
∴MN=MC+CN=$\frac{2}{3}$AC+$\frac{2}{3}$BC=$\frac{2}{3}$AB.
∵AB=90cm,
∴MN=$\frac{2}{3}$×90=60(cm).
(3)∵AB=90cm,BC=30cm,
∴AC=AB−BC=90−30=60(cm).
∵AM=$\frac{1}{3}$AC,
∴AM=$\frac{1}{3}$×60=20(cm),
∴MB=90−20=70(cm).
当点G在线段AB上时,
MG=MB−GB=70−15=55(cm);
当点G在线段AB的延长线上时,
MG=MB+GB=70+15=85(cm).
综上可知,MG的长度为55cm或85cm.
2. 如图,M,N 分别是 AC,CB 的中点。
(1) 若点 C 在线段 AB 上,$ AC = 12cm $,$ CB = 9cm $,求线段 MN 的长度。
(2) 若点 C 为线段 AB 上任意一点,且满足 $ AC + CB = acm $,其他条件不变,你能猜想出 MN 的长度吗?请你用一句简洁的话描述你发现的结论。
(3) 若点 C 在线段 AB 的延长线上,且满足 $ AC - CB = bcm $,M,N 分别为 AC,CB 的中点,你能猜想出线段 MN 的长度吗?请画出图形,写出你的结论,并说明理由。

(1) 若点 C 在线段 AB 上,$ AC = 12cm $,$ CB = 9cm $,求线段 MN 的长度。
(2) 若点 C 为线段 AB 上任意一点,且满足 $ AC + CB = acm $,其他条件不变,你能猜想出 MN 的长度吗?请你用一句简洁的话描述你发现的结论。
(3) 若点 C 在线段 AB 的延长线上,且满足 $ AC - CB = bcm $,M,N 分别为 AC,CB 的中点,你能猜想出线段 MN 的长度吗?请画出图形,写出你的结论,并说明理由。

答案:
2.解:(1)∵M,N分别是AC,CB的中点,
∴CM=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
∵AC=12cm,CB=9cm,
∴CM=6cm,NC=$\frac{9}{2}$cm,
∴MN=CM+NC=6+$\frac{9}{2}$=10.5(cm).
(2)∵M,N分别是AC,CB的中点,
∴CM=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,
∴MN=CM+NC=$\frac{1}{2}$(AC+CB).
∵AC+CB=acm,
∴MN=$\frac{a}{2}$cm.
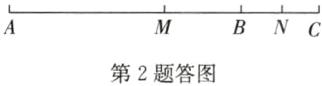
(3)画出图形如答图.MN=$\frac{b}{2}$cm,理由如下:
∵M,N分别是AC,CB的中点,
∴CM=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
∵MN=CM−CN,
∴MN=$\frac{1}{2}$(AC−CB).
∵AC−CB=bcm,
∴MN=$\frac{b}{2}$cm.
2.解:(1)∵M,N分别是AC,CB的中点,
∴CM=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
∵AC=12cm,CB=9cm,
∴CM=6cm,NC=$\frac{9}{2}$cm,
∴MN=CM+NC=6+$\frac{9}{2}$=10.5(cm).
(2)∵M,N分别是AC,CB的中点,
∴CM=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,
∴MN=CM+NC=$\frac{1}{2}$(AC+CB).
∵AC+CB=acm,
∴MN=$\frac{a}{2}$cm.
(3)画出图形如答图.MN=$\frac{b}{2}$cm,理由如下:
∵M,N分别是AC,CB的中点,
∴CM=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
∵MN=CM−CN,
∴MN=$\frac{1}{2}$(AC−CB).
∵AC−CB=bcm,
∴MN=$\frac{b}{2}$cm.
