1. 如图,已知点 A 在 x 轴的负半轴上,以 OA 为边在第二象限内作等边△AOB,点 M,N 分别为 OB,OA 边上的动点,以 MN 为边在 x 轴上方作等边△MNE,连接 OE,当∠EMO= 45°时,∠MEO 的度数为______.


答案:
$75^{\circ}$ 点拨:如答图,过点 $M$ 作 $MF// AB$ 交 $OA$ 于点 $F$.

∵$MF// AB$,∴$\angle MFO=\angle BAO=\angle AOB = 60^{\circ}$,
∴$\triangle MOF$ 为等边三角形,∴$\angle FMO = 60^{\circ},MF = MO$.
∵$\triangle MNE$ 是等边三角形,∴$\angle NME = 60^{\circ},MN = ME$,
∴$\angle FMN+\angle NMO=\angle NMO+\angle OME = 60^{\circ}$,
∴$\angle FMN=\angle OME$.
在 $\triangle MFN$ 和 $\triangle MOE$ 中, $\left\{\begin{array}{l}MF = MO,\\ \angle FMN=\angle OME,\\ MN = ME,\end{array}\right.$
∴$\triangle MFN\cong \triangle MOE(SAS)$,∴$\angle MFN=\angle MOE = 60^{\circ}$.
∵$\angle EMO = 45^{\circ}$,
∴$\angle MEO = 180^{\circ}-\angle MOE-\angle EMO$
$=180^{\circ}-60^{\circ}-45^{\circ}$
$=75^{\circ}$.
$75^{\circ}$ 点拨:如答图,过点 $M$ 作 $MF// AB$ 交 $OA$ 于点 $F$.

∵$MF// AB$,∴$\angle MFO=\angle BAO=\angle AOB = 60^{\circ}$,
∴$\triangle MOF$ 为等边三角形,∴$\angle FMO = 60^{\circ},MF = MO$.
∵$\triangle MNE$ 是等边三角形,∴$\angle NME = 60^{\circ},MN = ME$,
∴$\angle FMN+\angle NMO=\angle NMO+\angle OME = 60^{\circ}$,
∴$\angle FMN=\angle OME$.
在 $\triangle MFN$ 和 $\triangle MOE$ 中, $\left\{\begin{array}{l}MF = MO,\\ \angle FMN=\angle OME,\\ MN = ME,\end{array}\right.$
∴$\triangle MFN\cong \triangle MOE(SAS)$,∴$\angle MFN=\angle MOE = 60^{\circ}$.
∵$\angle EMO = 45^{\circ}$,
∴$\angle MEO = 180^{\circ}-\angle MOE-\angle EMO$
$=180^{\circ}-60^{\circ}-45^{\circ}$
$=75^{\circ}$.
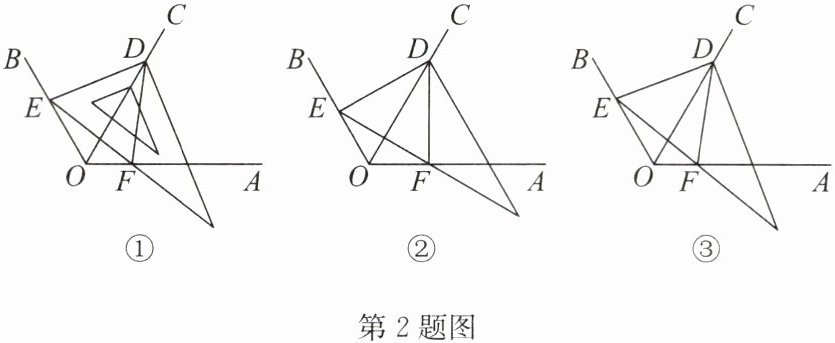
2. 如图①,已知∠AOB= 120°,OC 平分∠AOB.将直角三角板如图放置,使直角顶点 D 在 OC 上,60°角的顶点 E 在 OB 上,斜边与 OA 交于点 F(与点 O 不重合),连接 DF.
(1)如图②,若 DE⊥OB,求证:△DEF 为等边三角形;
(2)如图③,求证:OD= OE+OF.
(1)如图②,若 DE⊥OB,求证:△DEF 为等边三角形;
(2)如图③,求证:OD= OE+OF.

答案:
(1) ∵$DE\perp OB,\angle DEF = 60^{\circ},\therefore \angle OEF = 30^{\circ}$,
∴$\angle OFE = 180^{\circ}-\angle OEF-\angle EOF = 30^{\circ}$,
∴$\angle OEF=\angle OFE,\therefore OE = OF$.
∵$OC$ 平分 $\angle AOB,\therefore DO$ 垂直平分 $EF$,
∴$DE = DF,\therefore \triangle DEF$ 是等腰三角形.
又 ∵$\angle DEF = 60^{\circ},\therefore \triangle DEF$ 是等边三角形.
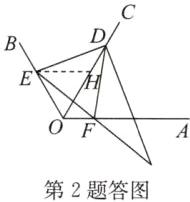
(2) 如答图,在线段 $OD$ 上截取 $OH = OE$, 连接 $EH$.
∵$\angle AOB = 120^{\circ},OC$ 平分 $\angle AOB,\therefore \angle EOD=\angle FOD = 60^{\circ}$
∵$OE = OH,\therefore \triangle OEH$ 是等边三角形,
∴$EH = OE = OH,\angle EHO = 60^{\circ}=\angle OEH=\angle DEF,\therefore \angle EHD = 120^{\circ}=\angle EOF,\angle DEH=\angle FEO$,
∴$\triangle DEH\cong \triangle FEO(ASA)$,
∴$DH = OF,\therefore OD = OH + DH = OE + OF$.
(1) ∵$DE\perp OB,\angle DEF = 60^{\circ},\therefore \angle OEF = 30^{\circ}$,
∴$\angle OFE = 180^{\circ}-\angle OEF-\angle EOF = 30^{\circ}$,
∴$\angle OEF=\angle OFE,\therefore OE = OF$.
∵$OC$ 平分 $\angle AOB,\therefore DO$ 垂直平分 $EF$,
∴$DE = DF,\therefore \triangle DEF$ 是等腰三角形.
又 ∵$\angle DEF = 60^{\circ},\therefore \triangle DEF$ 是等边三角形.
(2) 如答图,在线段 $OD$ 上截取 $OH = OE$, 连接 $EH$.
∵$\angle AOB = 120^{\circ},OC$ 平分 $\angle AOB,\therefore \angle EOD=\angle FOD = 60^{\circ}$
∵$OE = OH,\therefore \triangle OEH$ 是等边三角形,
∴$EH = OE = OH,\angle EHO = 60^{\circ}=\angle OEH=\angle DEF,\therefore \angle EHD = 120^{\circ}=\angle EOF,\angle DEH=\angle FEO$,
∴$\triangle DEH\cong \triangle FEO(ASA)$,
∴$DH = OF,\therefore OD = OH + DH = OE + OF$.
