1. 如图,在$\triangle ABC$中,$AB = AC$,$D$,$E是\triangle ABC$内的两点,$AD平分\angle BAC$,$\angle EBC= \angle E = 60^{\circ}$,若$BE = 6$,$DE = 2$,则$BC$的长度是 ( )

A.6
B.8
C.9
D.10

A.6
B.8
C.9
D.10
答案:
1.B 点拨:延长ED交BC于点M,延长AD交BC于点N,如答图.
∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN.
∵∠EBC=∠E=60°,∴△BEM为等边三角形,
∴BE=EM.
∵BE=6,DE=2,∴DM=EM−DE=6−2=4.
∵△BEM为等边三角形,∴∠EMB=60°.
∵AN⊥BC,∴∠DNM=90°,∴∠NDM=30°,
∴NM=2,∴BN=4,∴BC=2BN=8.

1.B 点拨:延长ED交BC于点M,延长AD交BC于点N,如答图.
∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN.
∵∠EBC=∠E=60°,∴△BEM为等边三角形,
∴BE=EM.
∵BE=6,DE=2,∴DM=EM−DE=6−2=4.
∵△BEM为等边三角形,∴∠EMB=60°.
∵AN⊥BC,∴∠DNM=90°,∴∠NDM=30°,
∴NM=2,∴BN=4,∴BC=2BN=8.

2. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,以点$A$为圆心,任意长为半径画弧分别交$AB$,$AC于点M$,$N$,再分别以点$M$,$N$为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧交于点$P$,连接$AP并延长交BC于点D$. 给出下列结论:①$AD是\angle BAC$的平分线;②$\angle ADC = 60^{\circ}$;③点$D在线段AB$的垂直平分线上;④$S_{\triangle DAC}:S_{\triangle ABC}= 1:3$. 其中正确结论的个数是 ( )
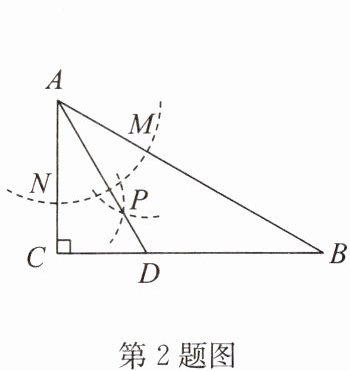
A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
2.D 点拨:①根据作图的过程可知,AD是∠BAC的平分线,故①正确.
②如答图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2= $\frac{1}{2}$∠CAB = 30°,
∴∠3=90°−∠2=60°,即∠ADC=60°.故②正确.

③∵∠1=∠B=30°,
∴AD=BD.
∴点D在线段AB的垂直平分线上.故③正确.
④如答图,∵在直角△ACD中,∠2=30°,
∴CD=$\frac{1}{2}$AD,
∴BC=CD+BD=$\frac{1}{2}$AD+AD=$\frac{3}{2}$AD.
∵S△DAC=$\frac{1}{2}$AC·CD=$\frac{1}{4}$AC·AD,
S△ABC=$\frac{1}{2}$AC·BC=$\frac{1}{2}$AC·$\frac{3}{2}$AD=$\frac{3}{4}$AC·AD,
∴S△DAC:S△ABC=($\frac{1}{4}$AC·AD):($\frac{3}{4}$AC·AD)=1:3.故④正确.
综上所述,正确的结论是①②③④,共4个.
2.D 点拨:①根据作图的过程可知,AD是∠BAC的平分线,故①正确.
②如答图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2= $\frac{1}{2}$∠CAB = 30°,
∴∠3=90°−∠2=60°,即∠ADC=60°.故②正确.

③∵∠1=∠B=30°,
∴AD=BD.
∴点D在线段AB的垂直平分线上.故③正确.
④如答图,∵在直角△ACD中,∠2=30°,
∴CD=$\frac{1}{2}$AD,
∴BC=CD+BD=$\frac{1}{2}$AD+AD=$\frac{3}{2}$AD.
∵S△DAC=$\frac{1}{2}$AC·CD=$\frac{1}{4}$AC·AD,
S△ABC=$\frac{1}{2}$AC·BC=$\frac{1}{2}$AC·$\frac{3}{2}$AD=$\frac{3}{4}$AC·AD,
∴S△DAC:S△ABC=($\frac{1}{4}$AC·AD):($\frac{3}{4}$AC·AD)=1:3.故④正确.
综上所述,正确的结论是①②③④,共4个.
3. 如图,在$\triangle ABC$中,$\angle C = 30^{\circ}$,$D是AC$的中点,$DE\perp AC交BC于点E$,点$O在ED$上,$OA = OB$,$OD = 2$,$OE = 4$,求$BE$的长.


答案:
3.解:如答图,连接OC,作OF⊥BC于点F.
由题意得DE=OD+OE=6.
在Rt△CDE中,∠DCE=30°,
∴CE=2DE=12,∠OEF=60°.
∵D是AC的中点,∴AD=DC.
∵ED⊥AC,∴OA=OC.
∵OA=OB,∴OB=OC;
∵OF⊥BC,∴CF=FB.
在Rt△OFE中,∠OEF=60°,
∴∠EOF=30°,
∴EF=$\frac{1}{2}$OE=2,
∴CF=CE−EF=10,∴BC=20,
∴BE=BC−CE=20−12=8.

3.解:如答图,连接OC,作OF⊥BC于点F.
由题意得DE=OD+OE=6.
在Rt△CDE中,∠DCE=30°,
∴CE=2DE=12,∠OEF=60°.
∵D是AC的中点,∴AD=DC.
∵ED⊥AC,∴OA=OC.
∵OA=OB,∴OB=OC;
∵OF⊥BC,∴CF=FB.
在Rt△OFE中,∠OEF=60°,
∴∠EOF=30°,
∴EF=$\frac{1}{2}$OE=2,
∴CF=CE−EF=10,∴BC=20,
∴BE=BC−CE=20−12=8.
