1. 已知$\triangle ABC$中,$\angle A = 40^{\circ}$,$\angle B和\angle C$都不是直角,高$BD和CE所在直线相交于点H$,则$\angle BHC$的度数为____.
答案:
140°或40° 点拨:①如答图①,当∠ACB为锐角时.
∵BD⊥AC,CE⊥AB,∴∠HDA=∠HEA=90°,
∴∠EHD=360°−∠A−∠HEA−∠HDA=360°−40°−90°−90°=140°,
∴∠BHC=∠EHD=140°.
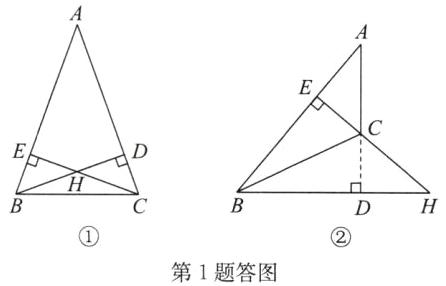
②如答图②,当∠ACB为钝角时.
∵BD⊥AC,CE⊥AB,∴∠AEC=∠HDC=90°,
∴∠ACE=90°−∠A=90°−40°=50°,
∴∠DCH=∠ACE=50°,
∴∠BHC=90°−∠DCH=90°−50°=40°.
综上可知,∠BHC的度数为140°或40°.
140°或40° 点拨:①如答图①,当∠ACB为锐角时.
∵BD⊥AC,CE⊥AB,∴∠HDA=∠HEA=90°,
∴∠EHD=360°−∠A−∠HEA−∠HDA=360°−40°−90°−90°=140°,
∴∠BHC=∠EHD=140°.

②如答图②,当∠ACB为钝角时.
∵BD⊥AC,CE⊥AB,∴∠AEC=∠HDC=90°,
∴∠ACE=90°−∠A=90°−40°=50°,
∴∠DCH=∠ACE=50°,
∴∠BHC=90°−∠DCH=90°−50°=40°.
综上可知,∠BHC的度数为140°或40°.
2. (2024春·房山区期末)在平面内,对于$\angle P和\angle Q$,给出如下定义:若存在一个常数$t(t>0)$,使得$\angle P + t\angle Q = 180^{\circ}$,则称$\angle Q是\angle P$的“$t$系数补角”.例如,$\angle P = 80^{\circ}$,$\angle Q = 20^{\circ}$,有$\angle P + 5\angle Q = 180^{\circ}$,则$\angle Q是\angle P$的“5系数补角”.
(1)若$\angle P = 90^{\circ}$,在$\angle 1 = 60^{\circ}$,$\angle 2 = 45^{\circ}$,$\angle 3 = 30^{\circ}$中,$\angle P$的“3系数补角”是____.
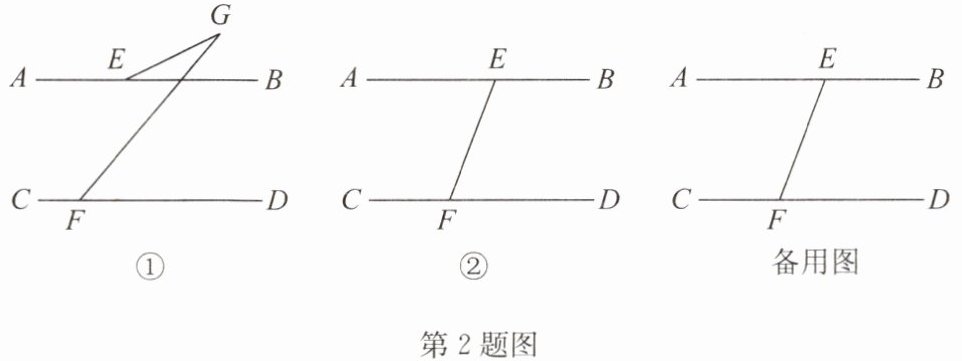
(2)在平面内,$AB// CD$,$E为直线AB$上一点,$F为直线CD$上一点.
①如图①,$G$为平面内一点,连接$GE$,$GF$,$\angle DFG = 50^{\circ}$,若$\angle BEG是\angle EGF$的“6系数补角”,求$\angle BEG$的大小;
②如图②,连接$EF$.若$H$为平面内一动点(点$H不在直线AB$,$CD$,$EF$上),$\angle EFH与\angle FEH两个角的平分线交于点M$.若$\angle BEH = \alpha$,$\angle DFH = \beta$,$\angle N是\angle EMF$的“2系数补角”,写出$\angle N$大小的所有情况(用含$\alpha和\beta$的代数式表示),并写出求解过程.
(1)若$\angle P = 90^{\circ}$,在$\angle 1 = 60^{\circ}$,$\angle 2 = 45^{\circ}$,$\angle 3 = 30^{\circ}$中,$\angle P$的“3系数补角”是____.
(2)在平面内,$AB// CD$,$E为直线AB$上一点,$F为直线CD$上一点.
①如图①,$G$为平面内一点,连接$GE$,$GF$,$\angle DFG = 50^{\circ}$,若$\angle BEG是\angle EGF$的“6系数补角”,求$\angle BEG$的大小;
②如图②,连接$EF$.若$H$为平面内一动点(点$H不在直线AB$,$CD$,$EF$上),$\angle EFH与\angle FEH两个角的平分线交于点M$.若$\angle BEH = \alpha$,$\angle DFH = \beta$,$\angle N是\angle EMF$的“2系数补角”,写出$\angle N$大小的所有情况(用含$\alpha和\beta$的代数式表示),并写出求解过程.

答案:
2. (1)∠3=30° 点拨:设∠P的“3系数补角”是x.
∵∠P=90°,∴∠P+3x=180°,
即90°+3x=180°,解得x=30°,
∴∠P的“3系数补角”是∠3=30°.
(2)解:①设∠BEG=m,∠EGF=n.
如答图①,设AB与GF相交于点H.
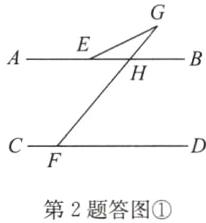
∵AB//CD,∠DFG=50°,
∴∠BHG=∠DFG=50°,
∴∠BEG+∠EGF=∠BHG=50°,即m+n=50°. ①
∵∠BEG是∠EGF的“6系数补角”,
∴∠EGF+6∠BEG=180°,即n+6m=180°. ②
联立①②得$\begin{cases}m + n = 50^{\circ}\\n + 6m = 180^{\circ}\end{cases}$,解得$\begin{cases}m = 26^{\circ}\\n = 24^{\circ}\end{cases}$,
即∠BEG的大小是26°.
②∵∠N是∠EMF的“2系数补角”,
∴∠EMF+2∠N=180°,∴∠N=90°−$\frac{1}{2}$∠EMF;

如答图②,∵∠EFH与∠FEH两个角的平分线交于点M ∴∠MEF=$\frac{1}{2}$∠HEF,∠MFE=$\frac{1}{2}$∠HFE;
∵∠EMF=180°−∠MEF−∠MFE
=180°−$\frac{1}{2}$(∠HEF+∠HFE)
=180°−$\frac{1}{2}$(180°−∠EHF)
=90°+$\frac{1}{2}$∠EHF;
过点H作HG//AB.
∵AB//CD,∴AB//CD//HG,
则∠EHG=∠AEH=180°−∠BEH=180°−α,
∠FHG=∠CFH=180°−∠DFH=180°−β,
∴∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(∠EHG+∠FHG)=90°+$\frac{1}{2}$(180°−α+180°−β)=270°−$\frac{1}{2}$(α+β),
∴∠N=90°−$\frac{1}{2}$∠EMF
=90°−$\frac{1}{2}$[270°−$\frac{1}{2}$(α+β)]
=$\frac{1}{4}$(α+β)−45°;
如答图③,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(α+β),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(α+β)]=45°−$\frac{1}{4}$(α+β);
如答图④,
∵AB//CD,∴∠1=∠DFH=β,
∴∠H=∠1−∠BEH=β−α,
∴∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(β−α),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(β−α)]=45°−$\frac{1}{4}$(β−α);
如答图⑤,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(α−β),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(α−β)]=45°−$\frac{1}{4}$(α−β);
如答图⑥,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(α−β),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(α−β)]=45°−$\frac{1}{4}$(α−β);
如答图⑦,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(β−α),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(β−α)]=45°−$\frac{1}{4}$(β−α).
综上可知,∠N的大小为$\frac{1}{4}$(α+β)−45°或45°−$\frac{1}{4}$(α+β)或45°−$\frac{1}{4}$(α−β)或45°−$\frac{1}{4}$(β−α).
2. (1)∠3=30° 点拨:设∠P的“3系数补角”是x.
∵∠P=90°,∴∠P+3x=180°,
即90°+3x=180°,解得x=30°,
∴∠P的“3系数补角”是∠3=30°.
(2)解:①设∠BEG=m,∠EGF=n.
如答图①,设AB与GF相交于点H.

∵AB//CD,∠DFG=50°,
∴∠BHG=∠DFG=50°,
∴∠BEG+∠EGF=∠BHG=50°,即m+n=50°. ①
∵∠BEG是∠EGF的“6系数补角”,
∴∠EGF+6∠BEG=180°,即n+6m=180°. ②
联立①②得$\begin{cases}m + n = 50^{\circ}\\n + 6m = 180^{\circ}\end{cases}$,解得$\begin{cases}m = 26^{\circ}\\n = 24^{\circ}\end{cases}$,
即∠BEG的大小是26°.
②∵∠N是∠EMF的“2系数补角”,
∴∠EMF+2∠N=180°,∴∠N=90°−$\frac{1}{2}$∠EMF;

如答图②,∵∠EFH与∠FEH两个角的平分线交于点M ∴∠MEF=$\frac{1}{2}$∠HEF,∠MFE=$\frac{1}{2}$∠HFE;
∵∠EMF=180°−∠MEF−∠MFE
=180°−$\frac{1}{2}$(∠HEF+∠HFE)
=180°−$\frac{1}{2}$(180°−∠EHF)
=90°+$\frac{1}{2}$∠EHF;
过点H作HG//AB.
∵AB//CD,∴AB//CD//HG,
则∠EHG=∠AEH=180°−∠BEH=180°−α,
∠FHG=∠CFH=180°−∠DFH=180°−β,
∴∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(∠EHG+∠FHG)=90°+$\frac{1}{2}$(180°−α+180°−β)=270°−$\frac{1}{2}$(α+β),
∴∠N=90°−$\frac{1}{2}$∠EMF
=90°−$\frac{1}{2}$[270°−$\frac{1}{2}$(α+β)]
=$\frac{1}{4}$(α+β)−45°;
如答图③,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(α+β),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(α+β)]=45°−$\frac{1}{4}$(α+β);
如答图④,
∵AB//CD,∴∠1=∠DFH=β,
∴∠H=∠1−∠BEH=β−α,
∴∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(β−α),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(β−α)]=45°−$\frac{1}{4}$(β−α);
如答图⑤,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(α−β),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(α−β)]=45°−$\frac{1}{4}$(α−β);
如答图⑥,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(α−β),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(α−β)]=45°−$\frac{1}{4}$(α−β);
如答图⑦,
同理可得,∠EMF=90°+$\frac{1}{2}$∠EHF=90°+$\frac{1}{2}$(β−α),
∴∠N=90°−$\frac{1}{2}$∠EMF=90°−$\frac{1}{2}$[90°+$\frac{1}{2}$(β−α)]=45°−$\frac{1}{4}$(β−α).
综上可知,∠N的大小为$\frac{1}{4}$(α+β)−45°或45°−$\frac{1}{4}$(α+β)或45°−$\frac{1}{4}$(α−β)或45°−$\frac{1}{4}$(β−α).