1. 能够
完全重合
的两个三角形叫作全等三角形.答案:完全重合
2. 全等三角形的性质:全等三角形的对应边
相等
,全等三角形的对应角相等
.答案:相等 相等
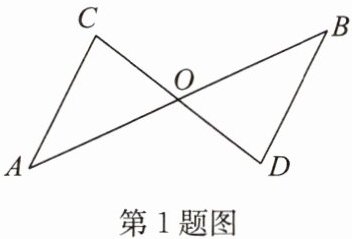
1. 如图,$\triangle AOC\cong \triangle BOD$,点$A与点B$是对应点,那么下列结论错误的是 (
A.$AB= CD$
B.$AC= BD$
C.$AO= BO$
D.$∠A= ∠B$
A
)
A.$AB= CD$
B.$AC= BD$
C.$AO= BO$
D.$∠A= ∠B$
答案:A
解析:
解:∵△AOC≌△BOD,点A与点B是对应点,
∴AC=BD,AO=BO,∠A=∠B,
∴选项B、C、D正确,选项A错误。
答案:A
∴AC=BD,AO=BO,∠A=∠B,
∴选项B、C、D正确,选项A错误。
答案:A
2. 下列说法错误的是 (
A.全等三角形的对应边相等
B.全等三角形的面积相等
C.全等三角形的对应角相等
D.全等三角形的角平分线相等
D
)A.全等三角形的对应边相等
B.全等三角形的面积相等
C.全等三角形的对应角相等
D.全等三角形的角平分线相等
答案:D
3. 已知$\triangle ABC\cong \triangle DEF$,且$\triangle DEF$的周长为 12. 若$AB= 5,BC= 4$,则$AC$的长为
3
.答案:3
解析:
解:∵△ABC≌△DEF,
∴△ABC的周长=△DEF的周长=12。
∵AB=5,BC=4,
∴AC=12 - AB - BC=12 - 5 - 4=3。
3
∴△ABC的周长=△DEF的周长=12。
∵AB=5,BC=4,
∴AC=12 - AB - BC=12 - 5 - 4=3。
3
4. 如图,$\triangle ABC\cong \triangle ADE,∠B= 42^{\circ },∠C= 30^{\circ },∠BAD= 50^{\circ }$,则$∠BAE$的度数为
58°
.答案:58°
解析:
解:在△ABC中,∠BAC=180°-∠B-∠C=180°-42°-30°=108°。
∵△ABC≌△ADE,
∴∠DAE=∠BAC=108°。
∵∠BAD=50°,
∴∠BAE=∠DAE-∠BAD=108°-50°=58°。
58°
∵△ABC≌△ADE,
∴∠DAE=∠BAC=108°。
∵∠BAD=50°,
∴∠BAE=∠DAE-∠BAD=108°-50°=58°。
58°
5. (2024春·河源期末)如图,已知$\triangle ABC\cong \triangle DBC,∠ABC= 55^{\circ },∠ACD= 60^{\circ }$,那么$∠D$的度数为
95°
.答案:95°
解析:
解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,∠ABC=∠DBC=55°,∠A=∠D。
∵∠ACD=∠ACB+∠DCB=60°,
∴∠ACB=∠DCB=30°。
在△ABC中,∠A=180°-∠ABC-∠ACB=180°-55°-30°=95°,
∴∠D=∠A=95°。
95°
∴∠ACB=∠DCB,∠ABC=∠DBC=55°,∠A=∠D。
∵∠ACD=∠ACB+∠DCB=60°,
∴∠ACB=∠DCB=30°。
在△ABC中,∠A=180°-∠ABC-∠ACB=180°-55°-30°=95°,
∴∠D=∠A=95°。
95°
6. 如图,$\triangle ABC\cong \triangle DEF$,点$B,F,C,E$在同一条直线上,$AC,DF交于点M,∠ACB= 30^{\circ }$,则$∠AMF$的度数是______
60°
.答案:60°
解析:
解:∵△ABC≌△DEF,
∴∠ACB=∠DFE=30°.
∵∠AMF是△MFC的外角,
∴∠AMF=∠ACB+∠DFE=30°+30°=60°.
60°
∴∠ACB=∠DFE=30°.
∵∠AMF是△MFC的外角,
∴∠AMF=∠ACB+∠DFE=30°+30°=60°.
60°
7. 如图,$\triangle ACF\cong \triangle ADE,AC= 6,AF= 2$,求$CE$的长.


答案:解:∵△ACF≌△ADE,∴AE=AF.∵AC=6,AF=2,∴CE=AC-AE=6-2=4.
8. 如图,已知$\triangle ABC\cong \triangle DEB$,点$E在AB$上,$AC与BD交于点F,AB= 6,BC= 3,∠C= 55^{\circ },∠D= 25^{\circ }$.
(1)求$AE$的长;
(2)求$∠AED$的度数.

(1)求$AE$的长;
(2)求$∠AED$的度数.

答案:(1)∵△ABC≌△DEB,∴EB=BC=3,∴AE=AB-EB=6-3=3.(2)∵△ABC≌△DEB,∴∠DBE=∠C=55°,∴∠AED=∠DBE+∠D=55°+25°=80°.