1.
三角形的一边与另一边的延长线组成的角
叫作三角形的外角。答案:三角形的一边与另一边的延长线组成的角
2. 三角形的外角等于
与它不相邻
的两个内角的和。答案:与它不相邻
1. 如果将一副三角板按如图的方式叠放,那么∠1的度数为(
A.$105^{\circ}$
B.$120^{\circ}$
C.$75^{\circ}$
D.$45^{\circ}$
A
)A.$105^{\circ}$
B.$120^{\circ}$
C.$75^{\circ}$
D.$45^{\circ}$
答案:A
解析:
解:由图可知,含45°角的三角板的45°角与含60°角的三角板的60°角相邻。
∠1为这两个角的外角,根据三角形外角等于不相邻两个内角之和,可得∠1 = 45° + 60° = 105°。
答案:A
∠1为这两个角的外角,根据三角形外角等于不相邻两个内角之和,可得∠1 = 45° + 60° = 105°。
答案:A
2. 如图,$\angle1= \angle2= 150^{\circ}$,则$\angle3$的度数为(
A.$30^{\circ}$
B.$150^{\circ}$
C.$120^{\circ}$
D.$60^{\circ}$
D
)A.$30^{\circ}$
B.$150^{\circ}$
C.$120^{\circ}$
D.$60^{\circ}$
答案:D
解析:
解:由邻补角定义,得
∠1的邻补角=180°-∠1=180°-150°=30°,
∠2的邻补角=180°-∠2=180°-150°=30°,
由三角形内角和定理,得
∠3=180°-30°-30°=120°。
答案:C
∠1的邻补角=180°-∠1=180°-150°=30°,
∠2的邻补角=180°-∠2=180°-150°=30°,
由三角形内角和定理,得
∠3=180°-30°-30°=120°。
答案:C
3. 如图,在$\triangle ABC$中,$\angle ABC= 40^{\circ}$,$\angle ACD= 76^{\circ}$,$BE平分\angle ABC$,$CE平分\angle ABC的外角\angle ACD$,则$\angle E$的度数为(
A.$40^{\circ}$
B.$36^{\circ}$
C.$20^{\circ}$
D.$18^{\circ}$
D
)A.$40^{\circ}$
B.$36^{\circ}$
C.$20^{\circ}$
D.$18^{\circ}$
答案:D
解析:
解:
∵BE平分∠ABC,∠ABC=40°,
∴∠EBC=∠ABC/2=40°/2=20°.
∵CE平分∠ACD,∠ACD=76°,
∴∠ECD=∠ACD/2=76°/2=38°.
∵∠ECD是△BCE的外角,
∴∠ECD=∠EBC+∠E.
∴∠E=∠ECD-∠EBC=38°-20°=18°.
答案:D
∵BE平分∠ABC,∠ABC=40°,
∴∠EBC=∠ABC/2=40°/2=20°.
∵CE平分∠ACD,∠ACD=76°,
∴∠ECD=∠ACD/2=76°/2=38°.
∵∠ECD是△BCE的外角,
∴∠ECD=∠EBC+∠E.
∴∠E=∠ECD-∠EBC=38°-20°=18°.
答案:D
4. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,点$D在边AB$上,将$\triangle BCD沿着直线CD$翻折,点$B的对应点E恰好落在边AC$上。如果$\angle A= 25^{\circ}$,那么$\angle ADE$的度数为
40°
。答案:40°
解析:
解:在$\triangle ABC$中,$\angle ACB=90^{\circ}$,$\angle A=25^{\circ}$,
$\angle B=90^{\circ}-\angle A=65^{\circ}$。
由翻折性质得:$\angle CED=\angle B=65^{\circ}$,$CE=CB$,$DE=DB$。
$\angle AED=180^{\circ}-\angle CED=115^{\circ}$。
在$\triangle AED$中,$\angle ADE=180^{\circ}-\angle A-\angle AED=180^{\circ}-25^{\circ}-115^{\circ}=40^{\circ}$。
故答案为:$40^{\circ}$。
$\angle B=90^{\circ}-\angle A=65^{\circ}$。
由翻折性质得:$\angle CED=\angle B=65^{\circ}$,$CE=CB$,$DE=DB$。
$\angle AED=180^{\circ}-\angle CED=115^{\circ}$。
在$\triangle AED$中,$\angle ADE=180^{\circ}-\angle A-\angle AED=180^{\circ}-25^{\circ}-115^{\circ}=40^{\circ}$。
故答案为:$40^{\circ}$。
5. 如图,$\angle A= 50^{\circ}$,$\angle B= 20^{\circ}$,$\angle D= 30^{\circ}$,则$\angle BCD$的度数为
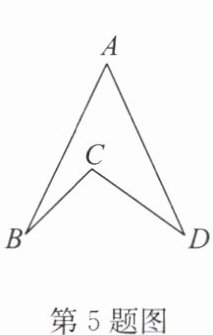
100°
。
答案:100°
6. 如图,在$\triangle ABC$中,$CD$是角平分线,$\angle A= 30^{\circ}$,$\angle CDB= 65^{\circ}$,求$\angle B$的度数。


答案:解:∵CD 平分∠ACB,∴∠ACB=2∠ACD.
∵∠CDB=∠A+∠ACD,
∴∠ACD=∠CDB-∠A=65°-30°=35°,
∴∠ACB=2∠ACD=70°.
∴∠B=180°-(∠A+∠ACB)=80°.
∵∠CDB=∠A+∠ACD,
∴∠ACD=∠CDB-∠A=65°-30°=35°,
∴∠ACB=2∠ACD=70°.
∴∠B=180°-(∠A+∠ACB)=80°.