1. 三角形三个内角的和等于
180°
.答案:180°
2. 直角三角形的两个锐角
互余
;有两个角互余
的三角形是直角三角形.答案:互余 互余
1. 若三角形有两个内角的和是$90^{\circ }$,则这个三角形是 (
A.钝角三角形
B.直角三角形
C.锐角三角形
D.不能确定
B
)A.钝角三角形
B.直角三角形
C.锐角三角形
D.不能确定
答案:B
解析:
解:因为三角形内角和为$180^{\circ}$,已知两个内角的和是$90^{\circ}$,所以第三个内角为$180^{\circ}-90^{\circ}=90^{\circ}$,有一个角是直角的三角形是直角三角形。
答案:B
答案:B
2. 在$\triangle ABC$中,若$∠A= 70^{\circ },∠B= 60^{\circ }$,则$∠C$的度数为 (
A.$50^{\circ }$
B.$60^{\circ }$
C.$70^{\circ }$
D.$80^{\circ }$
A
)A.$50^{\circ }$
B.$60^{\circ }$
C.$70^{\circ }$
D.$80^{\circ }$
答案:A
解析:
解:在△ABC中,∠A+∠B+∠C=180°
∵∠A=70°,∠B=60°
∴∠C=180°-∠A-∠B=180°-70°-60°=50°
答案:A
∵∠A=70°,∠B=60°
∴∠C=180°-∠A-∠B=180°-70°-60°=50°
答案:A
3. (2024春·江都区期末)如图,在$\triangle ABC$中,AD是$\triangle ABC$的高线,AE是$\triangle ABC$的角平分线. 若$∠B= 60^{\circ },∠C= 40^{\circ }$,则$∠DAE$的度数为
10°
.答案:10°
解析:
解:在$\triangle ABC$中,$\angle BAC=180^{\circ}-\angle B-\angle C=180^{\circ}-60^{\circ}-40^{\circ}=80^{\circ}$。
因为AE是角平分线,所以$\angle BAE=\frac{1}{2}\angle BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$。
因为AD是高线,所以$\angle ADB=90^{\circ}$,在$\triangle ABD$中,$\angle BAD=90^{\circ}-\angle B=90^{\circ}-60^{\circ}=30^{\circ}$。
则$\angle DAE=\angle BAE-\angle BAD=40^{\circ}-30^{\circ}=10^{\circ}$。
10°
因为AE是角平分线,所以$\angle BAE=\frac{1}{2}\angle BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$。
因为AD是高线,所以$\angle ADB=90^{\circ}$,在$\triangle ABD$中,$\angle BAD=90^{\circ}-\angle B=90^{\circ}-60^{\circ}=30^{\circ}$。
则$\angle DAE=\angle BAE-\angle BAD=40^{\circ}-30^{\circ}=10^{\circ}$。
10°
4. 如图,点E,F分别在AB,CD上,$∠B= 30^{\circ },∠C= 50^{\circ }$,则$∠1+∠2$的度数为
80°
.答案:80°
解析:
连接BC。
在△EBC中,∠B=30°,则∠EBC+∠BEC=180°-30°=150°。
在△FCB中,∠C=50°,则∠FCB+∠BFC=180°-50°=130°。
∠1=180°-∠BEC,∠2=180°-∠BFC。
∠1+∠2=360°-(∠BEC+∠BFC)=360°-(150°+130°-∠EBC-∠FCB)=360°-(280°-180°)=80°。
80°
在△EBC中,∠B=30°,则∠EBC+∠BEC=180°-30°=150°。
在△FCB中,∠C=50°,则∠FCB+∠BFC=180°-50°=130°。
∠1=180°-∠BEC,∠2=180°-∠BFC。
∠1+∠2=360°-(∠BEC+∠BFC)=360°-(150°+130°-∠EBC-∠FCB)=360°-(280°-180°)=80°。
80°
5. 如图,分别过$\triangle ABC$的顶点A,B作$AD// BE$. 若$∠CAD= 25^{\circ },∠EBC= 80^{\circ }$,则$∠ACB$的度数为
75°
.答案:75°
6. 在$\triangle ABC$中,若$∠A= 80^{\circ }$,BO平分$∠ABC$,CO平分$∠ACB$,则$∠BOC$的度数为
130°
.答案:130°
解析:
解:在△ABC中,∠A=80°,
∠ABC+∠ACB=180°-∠A=100°。
∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠ABC/2,∠OCB=∠ACB/2,
∠OBC+∠OCB=(∠ABC+∠ACB)/2=50°,
∠BOC=180°-(∠OBC+∠OCB)=130°。
130°
∠ABC+∠ACB=180°-∠A=100°。
∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠ABC/2,∠OCB=∠ACB/2,
∠OBC+∠OCB=(∠ABC+∠ACB)/2=50°,
∠BOC=180°-(∠OBC+∠OCB)=130°。
130°
7. 如图,已知AB,CD相交于点O,且$∠A= 38^{\circ },∠B= 58^{\circ },∠C= 44^{\circ }$,则$∠D$的度数是
64°
.答案:64°
解析:
解:在△AOD和△BOC中,
∠AOD=∠BOC(对顶角相等),
∠A+∠D+∠AOD=180°,∠B+∠C+∠BOC=180°,
所以∠A+∠D=∠B+∠C,
即38°+∠D=58°+44°,
∠D=58°+44°-38°=64°。
64°
∠AOD=∠BOC(对顶角相等),
∠A+∠D+∠AOD=180°,∠B+∠C+∠BOC=180°,
所以∠A+∠D=∠B+∠C,
即38°+∠D=58°+44°,
∠D=58°+44°-38°=64°。
64°
8. 已知$\triangle ABC的三个内角分别是∠A,∠B,∠C$,若$∠A= 60^{\circ },∠C= 2∠B$,则$∠C$的度数是
80°
.答案:80°
解析:
解:在△ABC中,∠A+∠B+∠C=180°
∵∠A=60°,∠C=2∠B
∴60°+∠B+2∠B=180°
3∠B=120°
∠B=40°
∠C=2∠B=80°
故∠C的度数是80°。
∵∠A=60°,∠C=2∠B
∴60°+∠B+2∠B=180°
3∠B=120°
∠B=40°
∠C=2∠B=80°
故∠C的度数是80°。
9. (2023·崇川区期末)如图,AD是$\triangle ABC$的高,$∠DAC= ∠C,∠B= 65^{\circ }$,求$∠BAC$的度数.
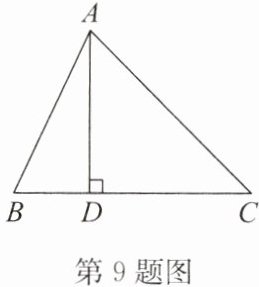

答案:解:∵AD是△ABC的高,∴∠ADB=∠ADC=90°,
∴∠B+∠BAD+∠ADB=180°,∠C+∠DAC+∠ADC=180°.
∵∠B=65°,∠DAC=∠C,
∴∠BAD=25°,∠DAC=∠C=45°,
∴∠BAC=∠BAD+∠DAC=70°.
∴∠B+∠BAD+∠ADB=180°,∠C+∠DAC+∠ADC=180°.
∵∠B=65°,∠DAC=∠C,
∴∠BAD=25°,∠DAC=∠C=45°,
∴∠BAC=∠BAD+∠DAC=70°.