1. 从三角形的顶点向它所对的边所在直线画垂线,所得线段叫作三角形的
高
。答案:高
2. 连接三角形的顶点和它所对的边的中点,所得线段叫作三角形的
中线
。三角形三条中线的交点叫作三角形的重心
。答案:中线 重心
3. 画三角形的一个角的平分线,与这个角所对的边相交,所得线段叫作三角形的
角平分线
。答案:角平分线
4. 三角形是具有
稳定性
的图形,而四边形没有稳定性。答案:稳定性
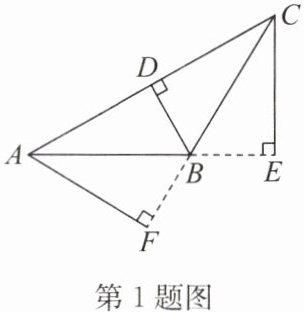
1. 如图,在$\triangle ABC$中,边$AB$上的高是(
A.$AF$
B.$BE$
C.$CE$
D.$BD$
C
)
A.$AF$
B.$BE$
C.$CE$
D.$BD$
答案:C
解析:
在$\triangle ABC$中,边$AB$上的高是从顶点$C$向边$AB$所在直线作的垂线段。由图可知,$CE \perp AB$于点$E$,所以边$AB$上的高是$CE$。
C
C
2. 如图,$CM是\triangle ABC$的中线,$AB = 10\mathrm{cm}$,则$BM$的长为(

A.$7\mathrm{cm}$
B.$6\mathrm{cm}$
C.$5\mathrm{cm}$
D.$4\mathrm{cm}$
C
)
A.$7\mathrm{cm}$
B.$6\mathrm{cm}$
C.$5\mathrm{cm}$
D.$4\mathrm{cm}$
答案:C
解析:
解:∵CM是△ABC的中线
∴M是AB的中点
∵AB=10cm
∴BM=AB/2=10/2=5cm
答案:C
∴M是AB的中点
∵AB=10cm
∴BM=AB/2=10/2=5cm
答案:C
3. 如图,点$D在线段BC$上,$AC\perp BC$,$AB = 8\mathrm{cm}$,$AD = 6\mathrm{cm}$,$AC = 4\mathrm{cm}$,则在$\triangle ABD$中,$BD$边上的高是

4
$\mathrm{cm}$。
答案:4
解析:
解:因为 $AC \perp BC$,所以 $\triangle ACD$ 和 $\triangle ACB$ 均为直角三角形。
在 $\triangle ACD$ 中,$AC = 4\mathrm{cm}$,$AD = 6\mathrm{cm}$,根据勾股定理:
$CD = \sqrt{AD^2 - AC^2} = \sqrt{6^2 - 4^2} = \sqrt{36 - 16} = \sqrt{20} = 2\sqrt{5}\mathrm{cm}$。
在 $\triangle ACB$ 中,$AC = 4\mathrm{cm}$,$AB = 8\mathrm{cm}$,根据勾股定理:
$BC = \sqrt{AB^2 - AC^2} = \sqrt{8^2 - 4^2} = \sqrt{64 - 16} = \sqrt{48} = 4\sqrt{3}\mathrm{cm}$。
则 $BD = BC - CD = 4\sqrt{3} - 2\sqrt{5}\mathrm{cm}$(此式虽不影响最终高的计算,但为完整逻辑链)。
在 $\triangle ABD$ 中,$BD$ 边上的高与 $AC$ 是同一条线段(因为 $AC \perp BC$,即 $AC$ 垂直于 $BD$ 所在的直线 $BC$),所以 $BD$ 边上的高为 $AC = 4\mathrm{cm}$。
答案:4
在 $\triangle ACD$ 中,$AC = 4\mathrm{cm}$,$AD = 6\mathrm{cm}$,根据勾股定理:
$CD = \sqrt{AD^2 - AC^2} = \sqrt{6^2 - 4^2} = \sqrt{36 - 16} = \sqrt{20} = 2\sqrt{5}\mathrm{cm}$。
在 $\triangle ACB$ 中,$AC = 4\mathrm{cm}$,$AB = 8\mathrm{cm}$,根据勾股定理:
$BC = \sqrt{AB^2 - AC^2} = \sqrt{8^2 - 4^2} = \sqrt{64 - 16} = \sqrt{48} = 4\sqrt{3}\mathrm{cm}$。
则 $BD = BC - CD = 4\sqrt{3} - 2\sqrt{5}\mathrm{cm}$(此式虽不影响最终高的计算,但为完整逻辑链)。
在 $\triangle ABD$ 中,$BD$ 边上的高与 $AC$ 是同一条线段(因为 $AC \perp BC$,即 $AC$ 垂直于 $BD$ 所在的直线 $BC$),所以 $BD$ 边上的高为 $AC = 4\mathrm{cm}$。
答案:4
4. 如图,以$AD$为高的三角形共有

6
个。
答案:6
解析:
解:以AD为高的三角形,其底边需在直线BC上,且顶点为A。
底边分别为:BD、BE、BC、ED、EC、DC。
对应的三角形为:△ABD、△ABE、△ABC、△AED、△AEC、△ADC。
共6个。
答案:6
底边分别为:BD、BE、BC、ED、EC、DC。
对应的三角形为:△ABD、△ABE、△ABC、△AED、△AEC、△ADC。
共6个。
答案:6
5. 如图。
(1)若$AD是\triangle ABC$的角平分线,则$\angle$
(2)若$AE是\triangle ABC$的中线,则
(3)若$AF是\triangle ABC$的高,则$\angle$
(1)若$AD是\triangle ABC$的角平分线,则$\angle$
BAD
$=\angle$DAC
$=\frac{1}{2}\angle$BAC
;(2)若$AE是\triangle ABC$的中线,则
BE
$=$EC
$=\frac{1}{2}$BC
;(3)若$AF是\triangle ABC$的高,则$\angle$
AFB
$=\angle$AFC
$=90^{\circ}$。答案:(1)BAD DAC BAC (2)BE EC BC (3)AFB AFC
6. 若$BD是\triangle ABC$的中线,$AC = 10\mathrm{cm}$,则$CD = $
5
$\mathrm{cm}$,$S_{\triangle ABC}:S_{\triangle BCD}= $2∶1
。答案:5 2∶1
解析:
解:因为BD是△ABC的中线,AC=10cm,
所以CD=AC/2=10/2=5cm。
因为△ABC和△BCD等底(BC)同高(从A、D到BC的距离,D为AC中点,距离比为2:1),
所以S△ABC:S△BCD=2:1。
5;2∶1
所以CD=AC/2=10/2=5cm。
因为△ABC和△BCD等底(BC)同高(从A、D到BC的距离,D为AC中点,距离比为2:1),
所以S△ABC:S△BCD=2:1。
5;2∶1