7. 下列时刻中,钟面上的时针和分针互相垂直的是(
A.2时30分
B.12时15分
C.6时15分
D.9时整
D
)A.2时30分
B.12时15分
C.6时15分
D.9时整
答案:D
解析:
钟面一周为360°,共分12个大格,每大格为30°。时针每小时走30°,每分钟走0.5°;分针每分钟走6°。
A.2时30分:时针与12时方向夹角为$2×30° + 30×0.5° = 75°$,分针与12时方向夹角为$30×6° = 180°$,夹角为$|180° - 75°| = 105°$,不垂直。
B.12时15分:时针与12时方向夹角为$15×0.5° = 7.5°$,分针与12时方向夹角为$15×6° = 90°$,夹角为$|90° - 7.5°| = 82.5°$,不垂直。
C.6时15分:时针与12时方向夹角为$6×30° + 15×0.5° = 187.5°$,分针与12时方向夹角为$15×6° = 90°$,夹角为$|187.5° - 90°| = 97.5°$,不垂直。
D.9时整:时针与12时方向夹角为$9×30° = 270°$,分针与12时方向夹角为0°,夹角为$|270° - 0°| = 90°$,垂直。
D
A.2时30分:时针与12时方向夹角为$2×30° + 30×0.5° = 75°$,分针与12时方向夹角为$30×6° = 180°$,夹角为$|180° - 75°| = 105°$,不垂直。
B.12时15分:时针与12时方向夹角为$15×0.5° = 7.5°$,分针与12时方向夹角为$15×6° = 90°$,夹角为$|90° - 7.5°| = 82.5°$,不垂直。
C.6时15分:时针与12时方向夹角为$6×30° + 15×0.5° = 187.5°$,分针与12时方向夹角为$15×6° = 90°$,夹角为$|187.5° - 90°| = 97.5°$,不垂直。
D.9时整:时针与12时方向夹角为$9×30° = 270°$,分针与12时方向夹角为0°,夹角为$|270° - 0°| = 90°$,垂直。
D
8. 下列各选项中,过直线$l外一点P画l$的垂线,三角尺操作正确的是(
D
)答案:D
9. (2024·张家港期末)已知$OA\perp OB$,直线$CD经过点O且\angle AOC = 40^{\circ}$,则$\angle BOD= $(
A.$50^{\circ}$
B.$130^{\circ}$
C.$50^{\circ}或130^{\circ}$
D.$40^{\circ}$
C
)A.$50^{\circ}$
B.$130^{\circ}$
C.$50^{\circ}或130^{\circ}$
D.$40^{\circ}$
答案:C
解析:
因为 $OA \perp OB$,所以 $\angle AOB = 90^\circ$。
情况一:直线 $CD$ 在 $\angle AOB$ 内部,
$\angle BOC = \angle AOB - \angle AOC = 90^\circ - 40^\circ = 50^\circ$,
$\angle BOD = \angle BOC = 50^\circ$。
情况二:直线 $CD$ 在 $\angle AOB$ 外部,
$\angle BOC = \angle AOB + \angle AOC = 90^\circ + 40^\circ = 130^\circ$,
$\angle BOD = \angle BOC = 130^\circ$。
综上,$\angle BOD = 50^\circ$ 或 $130^\circ$。
C
情况一:直线 $CD$ 在 $\angle AOB$ 内部,
$\angle BOC = \angle AOB - \angle AOC = 90^\circ - 40^\circ = 50^\circ$,
$\angle BOD = \angle BOC = 50^\circ$。
情况二:直线 $CD$ 在 $\angle AOB$ 外部,
$\angle BOC = \angle AOB + \angle AOC = 90^\circ + 40^\circ = 130^\circ$,
$\angle BOD = \angle BOC = 130^\circ$。
综上,$\angle BOD = 50^\circ$ 或 $130^\circ$。
C
10. (2024·溧水区期末)已知$\angle AOC = 140^{\circ}$,$OD平分\angle AOC$,$OB\perp OA于点O$,则$\angle BOD$的度数为
$20^{\circ }$或$160^{\circ }$
.答案:$20^{\circ }$或$160^{\circ }$
解析:
情况一:
$OB$在$\angle AOC$内部
$\because OD$平分$\angle AOC$,$\angle AOC=140^{\circ}$
$\therefore \angle AOD=\frac{1}{2}\angle AOC=70^{\circ}$
$\because OB\perp OA$
$\therefore \angle AOB=90^{\circ}$
$\angle BOD=\angle AOB-\angle AOD=90^{\circ}-70^{\circ}=20^{\circ}$
情况二:
$OB$在$\angle AOC$外部
$\angle BOD=\angle AOB+\angle AOD=90^{\circ}+70^{\circ}=160^{\circ}$
$20^{\circ}$或$160^{\circ}$
$OB$在$\angle AOC$内部
$\because OD$平分$\angle AOC$,$\angle AOC=140^{\circ}$
$\therefore \angle AOD=\frac{1}{2}\angle AOC=70^{\circ}$
$\because OB\perp OA$
$\therefore \angle AOB=90^{\circ}$
$\angle BOD=\angle AOB-\angle AOD=90^{\circ}-70^{\circ}=20^{\circ}$
情况二:
$OB$在$\angle AOC$外部
$\angle BOD=\angle AOB+\angle AOD=90^{\circ}+70^{\circ}=160^{\circ}$
$20^{\circ}$或$160^{\circ}$
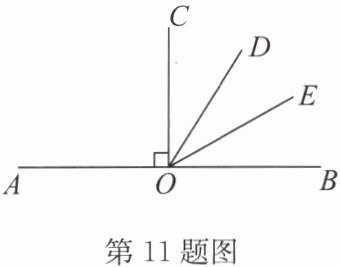
11. 如图,$OC\perp AB于点O$,射线$OD$,$OE在\angle BOC$内,$OE平分\angle BOD$,其中$\angle COD = 32^{\circ}$.
求:(1)$\angle BOD$的度数;
(2)$\angle AOE$的度数.
求:(1)$\angle BOD$的度数;
(2)$\angle AOE$的度数.

答案:解:
(1)因为$OC\perp AB$,所以$\angle AOC=\angle BOC=90^{\circ }$.
因为$\angle COD=32^{\circ }$,所以$\angle BOD=\angle BOC-\angle COD=90^{\circ }-32^{\circ }=58^{\circ }$.
(2)因为OE平分$\angle BOD$,所以$\angle BOE=\frac{1}{2}\angle BOD=29^{\circ }$,所以$\angle AOE=180^{\circ }-\angle BOE=180^{\circ }-29^{\circ }=151^{\circ }$.
(1)因为$OC\perp AB$,所以$\angle AOC=\angle BOC=90^{\circ }$.
因为$\angle COD=32^{\circ }$,所以$\angle BOD=\angle BOC-\angle COD=90^{\circ }-32^{\circ }=58^{\circ }$.
(2)因为OE平分$\angle BOD$,所以$\angle BOE=\frac{1}{2}\angle BOD=29^{\circ }$,所以$\angle AOE=180^{\circ }-\angle BOE=180^{\circ }-29^{\circ }=151^{\circ }$.
12. (2024·沭阳期末)如图,直线$AB$,$CD相交于点O$,$OF\perp CD$,$OE平分\angle BOD$.
(1)若$\angle AOC = 68^{\circ}$,求$\angle EOF$的度数;
(2)若$\angle BOE比\angle BOF大24^{\circ}$,求$\angle COE$的度数.

(1)若$\angle AOC = 68^{\circ}$,求$\angle EOF$的度数;
(2)若$\angle BOE比\angle BOF大24^{\circ}$,求$\angle COE$的度数.

答案:解:
(1)因为$OF\perp CD$,所以$\angle COF=\angle DOF=90^{\circ }$.
因为直线AB,CD相交于点O,$\angle AOC=68^{\circ }$,
所以$\angle BOD=\angle AOC=68^{\circ }$.
因为OE平分$\angle BOD$,所以$\angle DOE=\frac{1}{2}\angle BOD=34^{\circ }$,所以$\angle EOF=\angle DOF-\angle DOE=90^{\circ }-34^{\circ }=56^{\circ }$.
(2)设$\angle BOF=x^{\circ }$,则$\angle DOE=\angle BOE=(x+24)^{\circ }$,
根据题意,得$2(x+24)+x=90$,解得$x=14$,
所以$\angle DOE=(x+24)^{\circ }=38^{\circ }$,
所以$\angle COE=\angle COD-\angle DOE=180^{\circ }-38^{\circ }=142^{\circ }$.
(1)因为$OF\perp CD$,所以$\angle COF=\angle DOF=90^{\circ }$.
因为直线AB,CD相交于点O,$\angle AOC=68^{\circ }$,
所以$\angle BOD=\angle AOC=68^{\circ }$.
因为OE平分$\angle BOD$,所以$\angle DOE=\frac{1}{2}\angle BOD=34^{\circ }$,所以$\angle EOF=\angle DOF-\angle DOE=90^{\circ }-34^{\circ }=56^{\circ }$.
(2)设$\angle BOF=x^{\circ }$,则$\angle DOE=\angle BOE=(x+24)^{\circ }$,
根据题意,得$2(x+24)+x=90$,解得$x=14$,
所以$\angle DOE=(x+24)^{\circ }=38^{\circ }$,
所以$\angle COE=\angle COD-\angle DOE=180^{\circ }-38^{\circ }=142^{\circ }$.