1. (北京通州区·几何直观)在右图的平行四边形中,梯形的面积是三角形面积的(
A.6倍
B.5倍
C.4倍
D.3倍
]
B
)。A.6倍
B.5倍
C.4倍
D.3倍
]
答案:B 【提示】观察图形可知,梯形的高与三角形的高相等,梯形上底和下底的和是三角形底的5倍。
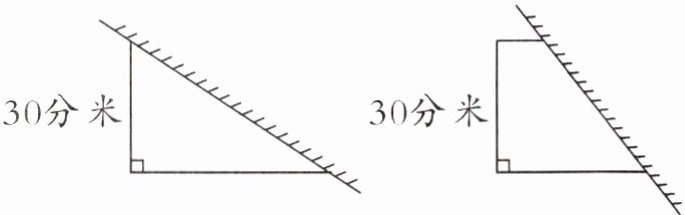
2. (南通通州区·几何直观)李奶奶和王大爷用同样长的篱笆,一面靠墙围菜园。李奶奶围成了一个三角形,王大爷围成了一个梯形。两个菜园的面积相比,(
A.三角形面积大
B.梯形面积大
C.一样大
D.无法判断
C
)。
A.三角形面积大
B.梯形面积大
C.一样大
D.无法判断
答案:C 【提示】三角形的面积=底×高÷2;梯形的面积=(上底+下底)×高÷2;高一样,三角形的底与梯形上、下底的和相等,所以面积一样大。
3. (无锡惠山区·几何直观)下图是由6个面积是4平方厘米的正方形组成的,三角形C的面积是(
4
)平方厘米,空白部分的面积是(16
)平方厘米。答案:4 16 【提示】三角形C的面积与一个正方形的面积相等,空白部分的面积等于4个小正方形的面积。
解析:
三角形C的面积是4平方厘米,空白部分的面积是16平方厘米。
4. (连云港赣榆区·几何直观)我国古代数学名著《九章算术》中记载了三角形面积的计算方法是“半广以乘正从”(“广”指三角形的底,“从”指三角形的高)。我国数学家刘徽在注文中还用“以盈补虚”的方法加以说明(如右图)。
如果三角形的底是14厘米,高是5厘米,那么转化成的长方形的长是(
]

如果三角形的底是14厘米,高是5厘米,那么转化成的长方形的长是(
7
)厘米,宽是(5
)厘米,面积是(35
)平方厘米。]

答案:7 5 35 【提示】观察图形可知,长方形的宽等于三角形的高,长方形的长等于三角形底的一半,即14÷2=7(厘米),所以面积是7×5=35(平方厘米)。
解析:
7 5 35
5. (泰州姜堰区·几何直观)把一幅七巧板按如图①所示进行1~7编号,1~7号分别对应着七巧板的七块。如图②所示的“天鹅”是由这幅七巧板拼成的,“天鹅”头颈由3号和6号块构成,其面积为$3dm^2,$则图①大正方形的边长为(
4
)dm。答案:4 【提示】由3号和6号图形的面积和是3 dm²,推出整个正方形的面积是16 dm²,由此得到大正方形的边长是4 dm。
6. (泰州市)有一块平行四边形菜地(如图),DE= EF= FC,BD= 3GB,三角形GEF种的是小白菜,面积是8平方米,求这块平行四边形菜地的面积。
]

]

答案:3×8=24(平方米) 24÷2=12(平方米)(24+12)×2=72(平方米)
【提示】连接GC。因为DE=EF=FC,所以S三角形DEG=S三角形GEF=S三角形CFG=8(平方米),S三角形DCG=3S三角形GEF=3×8=24(平方米),又因为BD=3GB,所以三角形DCG的面积是三角形BGC面积的3-1=2倍,即三角形BGC的面积是24÷2=12(平方米),由此可知平行四边形菜地的面积是(24+12)×2=72(平方米)。
【提示】连接GC。因为DE=EF=FC,所以S三角形DEG=S三角形GEF=S三角形CFG=8(平方米),S三角形DCG=3S三角形GEF=3×8=24(平方米),又因为BD=3GB,所以三角形DCG的面积是三角形BGC面积的3-1=2倍,即三角形BGC的面积是24÷2=12(平方米),由此可知平行四边形菜地的面积是(24+12)×2=72(平方米)。
7. (淮安淮阴区)下图中长方形纸条准备从正方形的左边水平移动到右边,平均每秒移动2厘米。

(1)长方形完全移动到正方形的右边需要多少秒?
(2)如果移动4秒停下,那么这时重叠部分的面积是多少平方厘米?

(1)长方形完全移动到正方形的右边需要多少秒?
(2)如果移动4秒停下,那么这时重叠部分的面积是多少平方厘米?
答案:
(1)(20+10)÷2=15(秒) 【提示】这是一个“火车过桥”问题,长方形完全移动到正方形的右边,移动的总长度是20+10=30(厘米)。
(2)4×2=8(厘米) 8×2=16(平方厘米)
【提示】移动4秒后,重叠的部分是长方形,只要找出这个长方形的长和宽就能知道重叠部分的面积。因为每秒移动2厘米,所以4秒移动了2×4=8(厘米),又因为宽是2厘米,所以重叠部分的面积是8×2=16(平方厘米)。
(1)(20+10)÷2=15(秒) 【提示】这是一个“火车过桥”问题,长方形完全移动到正方形的右边,移动的总长度是20+10=30(厘米)。
(2)4×2=8(厘米) 8×2=16(平方厘米)
【提示】移动4秒后,重叠的部分是长方形,只要找出这个长方形的长和宽就能知道重叠部分的面积。因为每秒移动2厘米,所以4秒移动了2×4=8(厘米),又因为宽是2厘米,所以重叠部分的面积是8×2=16(平方厘米)。