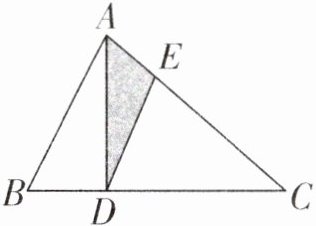
例 如下图,在三角形 ABC 中,DC= 2BD,CE= 3AE,涂色部分的面积是 20 平方厘米,求三角形 ABC 的面积。
解析
在三角形 ADC 中,CE 是 AE 的 3 倍,则三角形 DEC 的面积是三角形 ADE 面积的 3 倍,三角形 DEC 的面积为 20×3= 60(平方厘米),三角形 ADC 的面积为 20+60= 80(平方厘米);因为 DC 是 BD 的 2 倍,所以三角形 ADC 的面积是三角形 ABD 面积的 2 倍,三角形 ABD 的面积为 80÷2= 40(平方厘米),三角形 ABC 的面积为 40+80= 120(平方厘米)。
答案:20×(1+3)= 80(平方厘米)
80÷2+80= 120(平方厘米)
答:三角形 ABC 的面积是 120 平方厘米。

解析
在三角形 ADC 中,CE 是 AE 的 3 倍,则三角形 DEC 的面积是三角形 ADE 面积的 3 倍,三角形 DEC 的面积为 20×3= 60(平方厘米),三角形 ADC 的面积为 20+60= 80(平方厘米);因为 DC 是 BD 的 2 倍,所以三角形 ADC 的面积是三角形 ABD 面积的 2 倍,三角形 ABD 的面积为 80÷2= 40(平方厘米),三角形 ABC 的面积为 40+80= 120(平方厘米)。
答案:20×(1+3)= 80(平方厘米)
80÷2+80= 120(平方厘米)
答:三角形 ABC 的面积是 120 平方厘米。
答案:在三角形ADC中,CE=3AE,涂色部分(三角形ADE)面积为20平方厘米,所以三角形DEC面积为20×3=60平方厘米,三角形ADC面积为20+60=80平方厘米。
因为DC=2BD,所以三角形ABD面积为80÷2=40平方厘米。
三角形ABC面积为40+80=120平方厘米。
答:三角形ABC的面积是120平方厘米。
因为DC=2BD,所以三角形ABD面积为80÷2=40平方厘米。
三角形ABC面积为40+80=120平方厘米。
答:三角形ABC的面积是120平方厘米。
1. 如下图,在三角形 ABC 中,BD= DF= FC,BE= EA。若三角形 BDE 的面积是 6 平方厘米,三角形 ABC 的面积是(

A.36
B.18
C.24
D.30
A
)平方厘米。
A.36
B.18
C.24
D.30
答案:1. A 【提示】接连 EC,三角形 BDE、三角形 DEF、三角形 EFC 等底等高。面积都是 6 平方厘米,三角形 BEC 的面积就是 18 平方厘米。三角形 BEC 与三角形 AEC 等底等高,面积都是 18 平方厘米,三角形 ABC 的面积就是 36 平方厘米。
2. 如右下图,图中 BO= 2DO,涂色部分的面积是 4 平方厘米,求梯形 ABCD 的面积。


答案:2. 4÷2+4×2+4+4=18(平方厘米)
【提示】因为 BO 是 DO 的 2 倍,三角形 BOC 与三角形 COD 的高一样,所以三角形 BOC 的面积是三角形 COD 的 2 倍,三角形 COD 面积是 4÷2=2(平方厘米);又因为三角形 BOC 的面积和三角形 DOA 的面积一样,同理可知,三角形 AOB 的面积是三角形 DOA 的 2 倍,三角形 AOB 的面积是 4×2=8(平方厘米),这样把梯形中 4 个三角形的面积相加即可。
【提示】因为 BO 是 DO 的 2 倍,三角形 BOC 与三角形 COD 的高一样,所以三角形 BOC 的面积是三角形 COD 的 2 倍,三角形 COD 面积是 4÷2=2(平方厘米);又因为三角形 BOC 的面积和三角形 DOA 的面积一样,同理可知,三角形 AOB 的面积是三角形 DOA 的 2 倍,三角形 AOB 的面积是 4×2=8(平方厘米),这样把梯形中 4 个三角形的面积相加即可。
3. 如右下图,长方形 ABCD 的面积是 16 平方厘米,E、F 都是所在边的中点,求三角形 AEF(涂色部分)的面积。


答案:3. 16-(16÷4+16÷4+16÷8)=6(平方厘米)
【提示】因为 E、F 都是所在边的中点,所以三角形 ADF 和三角形 ABE 的面积各占长方形面积的$\frac{1}{4}$,三角形 EFC 的面积是长方形面积的$\frac{1}{8}$,从长方形面积里减去这 3 个三角形的面积和,就能得到三角形 AEF 的面积。
【提示】因为 E、F 都是所在边的中点,所以三角形 ADF 和三角形 ABE 的面积各占长方形面积的$\frac{1}{4}$,三角形 EFC 的面积是长方形面积的$\frac{1}{8}$,从长方形面积里减去这 3 个三角形的面积和,就能得到三角形 AEF 的面积。
4. 如右下图,在四边形 ABCD 中,M 为 AB 的中点,N 为 CD 的中点,四边形 ABCD 的面积是 80 平方厘米,则四边形 BND M 的面积是多少平方厘米?


答案:4. 80÷2=40(平方厘米) 【提示】连接 BD,因为 M 是 AB 的中点,所以三角形 AMD 和三角形 BMD 等底等高;同理,三角形 DBN 和三角形 BNC 也等底等高。据此可知四边形 BND M 的面积是四边形 ABCD 面积的一半。
解析:
连接 BD。
因为 M 是 AB 的中点,所以 $ S_{\triangle AMD}=S_{\triangle BMD} $。
因为 N 是 CD 的中点,所以 $ S_{\triangle DBN}=S_{\triangle BNC} $。
则 $ S_{四边形BNDM}=S_{\triangle BMD}+S_{\triangle DBN}=\frac{1}{2}S_{\triangle ABD}+\frac{1}{2}S_{\triangle BCD}=\frac{1}{2}(S_{\triangle ABD}+S_{\triangle BCD})=\frac{1}{2}S_{四边形ABCD} $。
$ S_{四边形BNDM}=\frac{1}{2}×80=40 $(平方厘米)。
答案:40
因为 M 是 AB 的中点,所以 $ S_{\triangle AMD}=S_{\triangle BMD} $。
因为 N 是 CD 的中点,所以 $ S_{\triangle DBN}=S_{\triangle BNC} $。
则 $ S_{四边形BNDM}=S_{\triangle BMD}+S_{\triangle DBN}=\frac{1}{2}S_{\triangle ABD}+\frac{1}{2}S_{\triangle BCD}=\frac{1}{2}(S_{\triangle ABD}+S_{\triangle BCD})=\frac{1}{2}S_{四边形ABCD} $。
$ S_{四边形BNDM}=\frac{1}{2}×80=40 $(平方厘米)。
答案:40