例 每年的 12 月 4 日是“国家宪法日”。今年“国家宪法日”学校组织开展“宪法小卫士”知识竞赛活动,每人需要答完 20 题,按竞赛规则规定:答对一题得 5 分,答错一题倒扣 2 分。
(1)如果答对一题记作+5 分,那么答错一题记作什么?答对一题和答错一题相差多少分?
(2)如果小明在这次竞赛中答完全部题目得了 79 分,那么他答对了多少题?
解析
(1)答对用正数表示,一题得 5 分,记作+5 分。答错用负数表示,一题倒扣 2 分,记作-2 分。一对一错相差 $5+2= 7$(分)。
(2)先假设 20 题全部答对,满分 $20×5= 100$(分),少得 $100-79= 21$(分),每答错一题要少得 $5+2= 7$(分),可求出答错 $21÷7= 3$(题),进而即可求出答错题的数量。
答案:(1)答错一题记作-2 分
相差:$5+2= 7$(分)
(2)$(20×5-79)÷7= 3$(题)
$20-3= 17$(题)
答:他答对了 17 题。
(1)如果答对一题记作+5 分,那么答错一题记作什么?答对一题和答错一题相差多少分?
(2)如果小明在这次竞赛中答完全部题目得了 79 分,那么他答对了多少题?
解析
(1)答对用正数表示,一题得 5 分,记作+5 分。答错用负数表示,一题倒扣 2 分,记作-2 分。一对一错相差 $5+2= 7$(分)。
(2)先假设 20 题全部答对,满分 $20×5= 100$(分),少得 $100-79= 21$(分),每答错一题要少得 $5+2= 7$(分),可求出答错 $21÷7= 3$(题),进而即可求出答错题的数量。
答案:(1)答错一题记作-2 分
相差:$5+2= 7$(分)
(2)$(20×5-79)÷7= 3$(题)
$20-3= 17$(题)
答:他答对了 17 题。
答案:解析:
(1) 根据题意,答对一题得 5 分,用正数表示,即+5 分。答错一题倒扣 2 分,用负数表示,即-2 分。因此,答对一题和答错一题相差的分数是 $5 + 2 = 7$ 分。
(2) 假设小明全部答对,则满分是 $20 × 5 = 100$ 分。但他实际得了 79 分,所以他少得了 $100 - 79 = 21$ 分。每答错一题,他不仅少得 5 分,还要被扣掉 2 分,所以总共少得 7 分。因此,他答错的题目数量是 $21 ÷ 7 = 3$ 题。总题数是 20 题,所以他答对的题目数量是 $20 - 3 = 17$ 题。
答案:
(1) 答错一题记作 -2 分;答对一题和答错一题相差 7 分。
(2) 他答对了 17 题。
(1) 根据题意,答对一题得 5 分,用正数表示,即+5 分。答错一题倒扣 2 分,用负数表示,即-2 分。因此,答对一题和答错一题相差的分数是 $5 + 2 = 7$ 分。
(2) 假设小明全部答对,则满分是 $20 × 5 = 100$ 分。但他实际得了 79 分,所以他少得了 $100 - 79 = 21$ 分。每答错一题,他不仅少得 5 分,还要被扣掉 2 分,所以总共少得 7 分。因此,他答错的题目数量是 $21 ÷ 7 = 3$ 题。总题数是 20 题,所以他答对的题目数量是 $20 - 3 = 17$ 题。
答案:
(1) 答错一题记作 -2 分;答对一题和答错一题相差 7 分。
(2) 他答对了 17 题。
1. 学校进行安全素养测试,共有 20 题。规则:答对一题得 5 分,答错或不答得-2 分。小明在前 15 题中,答对 12 题,剩下的题目他选择弃权。小明这次安全素养测试得了(
44
)分。答案:44 【提示】先算出答对的分数,用答对的题数乘每题的分数,再减去扣去的分数,扣去的分数等于答错或者不答的题数乘每题扣的分数,即可解答。
解析:
12×5=60
(15-12)+(20-15)=3+5=8
8×2=16
60-16=44
44
(15-12)+(20-15)=3+5=8
8×2=16
60-16=44
44
2. 一次自我测验中,共有 20 道选择题,每道题答对得 5 分,答错或不答不仅不得分,还要倒扣分。如果亮亮答对 19 道题,得分是 94 分,那么点点答对了 16 道题,他得了(
A.79
B.76
C.56
76
)分。A.79
B.76
C.56
答案:B 【提示】亮亮答对19道题,得分应该是19×5=95(分),实际得分是94分,说明答错1题或不答倒扣的分数是95-94=1(分)。点点答对了16道题应得16×5=80(分),但是答错了20-16=4(道)题要倒扣4×1=4(分),所以他实际得了80-4=76(分)。
3. 某运输队运送瓷器 500 箱,每箱装有 6 件瓷器,已知每件瓷器的运费为 1 元,如果在运输过程中损坏一件瓷器,那么不但得不到运费还要赔偿 7 元。最后结账时,运输队共得 2360 元。在运输过程中一共损坏了多少件瓷器?
答案:500×6×1=3000(元)
(3000-2360)÷(1+7)=80(件)
【提示】可以假设全部安全运到了目的地,则可得运费500×6×1=3000(元),而实际只得2360元,相差3000-2360=640(元),说明有损坏的,每损坏一件就少收1+7=8(元),相差的640元里面有多少个8元就损坏了多少件,即640÷8=80(件)。
(3000-2360)÷(1+7)=80(件)
【提示】可以假设全部安全运到了目的地,则可得运费500×6×1=3000(元),而实际只得2360元,相差3000-2360=640(元),说明有损坏的,每损坏一件就少收1+7=8(元),相差的640元里面有多少个8元就损坏了多少件,即640÷8=80(件)。
4. 实验小学五年级举行足球比赛,下表是积分规则:
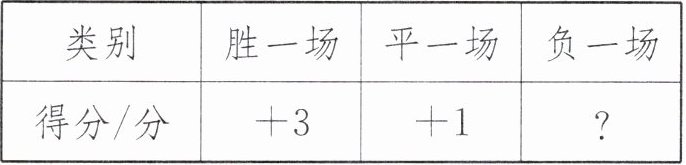
(1)五(1)班的比赛结果是 2 胜 1 平 3 负,五(1)班的得分共计 1 分。负一场得分表示为多少?
(2)五(2)班的得分是 7 分,你能推算出五(2)班的比赛结果是怎样的吗?

(1)五(1)班的比赛结果是 2 胜 1 平 3 负,五(1)班的得分共计 1 分。负一场得分表示为多少?
(2)五(2)班的得分是 7 分,你能推算出五(2)班的比赛结果是怎样的吗?
答案:
(1)2×3+1-1=6(分) 6÷3=2(分) -2
(2)答案不唯一,如:胜3场,负1场,平的场次为0。
【提示】由
(1)可求出负一场扣2分,根据最后得分,可以预测五
(2)班胜负平的场次。
(1)2×3+1-1=6(分) 6÷3=2(分) -2
(2)答案不唯一,如:胜3场,负1场,平的场次为0。
【提示】由
(1)可求出负一场扣2分,根据最后得分,可以预测五
(2)班胜负平的场次。