例 从楼下走过一些台阶到楼上,规定每一步只能跨1级或2级台阶。从楼下到楼上共10级台阶,有多少种不同的走法?
解析
只有1级台阶有1种走法;只有2级台阶有2种走法;只有3级台阶有3种走法;只有4级台阶有5种走法(迈第1步时可跨1级,也可跨2级,即分成两类:第1步跨1级还剩3级,上面已知3级台阶有3种走法;第1步跨2级还剩2级,上面已知2级台阶有2种走法,所以4级台阶共有3+2= 5(种)走法)。其递推公式为每一项(大于2)等于前两项的和,规律为:
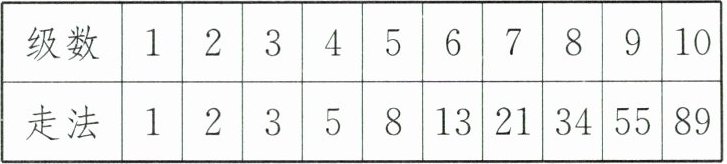
答案:有89种不同的走法。
解析
只有1级台阶有1种走法;只有2级台阶有2种走法;只有3级台阶有3种走法;只有4级台阶有5种走法(迈第1步时可跨1级,也可跨2级,即分成两类:第1步跨1级还剩3级,上面已知3级台阶有3种走法;第1步跨2级还剩2级,上面已知2级台阶有2种走法,所以4级台阶共有3+2= 5(种)走法)。其递推公式为每一项(大于2)等于前两项的和,规律为:

答案:有89种不同的走法。
答案:解析:
本题可通过分析前几级台阶的走法数量,找出其规律,进而得出$10$级台阶的不同走法数量。
已知只有$1$级台阶时,有$1$种走法;只有$2$级台阶时,有$2$种走法;只有$3$级台阶时,走第$1$步可跨$1$级,也可跨$2$级。若第$1$步跨$1$级,还剩$2$级,$2$级台阶有$2$种走法;若第$1$步跨$2$级,还剩$1$级,$1$级台阶有$1$种走法,所以$3$级台阶共有$1 + 2 = 3$(种)走法。同理,$4$级台阶时,第$1$步跨$1$级,还剩$3$级,$3$级台阶有$3$种走法;第$1$步跨$2$级,还剩$2$级,$2$级台阶有$2$种走法,所以$4$级台阶共有$3 + 2 = 5$(种)走法。
由此可归纳出递推公式:每一项(大于$2$)等于前两项的和,即$a_{n}=a_{n - 1}+a_{n - 2}$($n\geq3$,$a_{n}$表示$n$级台阶的走法数量)。
根据此规律依次计算可得:
$5$级台阶的走法有$5 + 3 = 8$(种);
$6$级台阶的走法有$8 + 5 = 13$(种);
$7$级台阶的走法有$13 + 8 = 21$(种);
$8$级台阶的走法有$21 + 13 = 34$(种);
$9$级台阶的走法有$34 + 21 = 55$(种);
$10$级台阶的走法有$55 + 34 = 89$(种)。
答案:有$89$种不同的走法。
本题可通过分析前几级台阶的走法数量,找出其规律,进而得出$10$级台阶的不同走法数量。
已知只有$1$级台阶时,有$1$种走法;只有$2$级台阶时,有$2$种走法;只有$3$级台阶时,走第$1$步可跨$1$级,也可跨$2$级。若第$1$步跨$1$级,还剩$2$级,$2$级台阶有$2$种走法;若第$1$步跨$2$级,还剩$1$级,$1$级台阶有$1$种走法,所以$3$级台阶共有$1 + 2 = 3$(种)走法。同理,$4$级台阶时,第$1$步跨$1$级,还剩$3$级,$3$级台阶有$3$种走法;第$1$步跨$2$级,还剩$2$级,$2$级台阶有$2$种走法,所以$4$级台阶共有$3 + 2 = 5$(种)走法。
由此可归纳出递推公式:每一项(大于$2$)等于前两项的和,即$a_{n}=a_{n - 1}+a_{n - 2}$($n\geq3$,$a_{n}$表示$n$级台阶的走法数量)。
根据此规律依次计算可得:
$5$级台阶的走法有$5 + 3 = 8$(种);
$6$级台阶的走法有$8 + 5 = 13$(种);
$7$级台阶的走法有$13 + 8 = 21$(种);
$8$级台阶的走法有$21 + 13 = 34$(种);
$9$级台阶的走法有$34 + 21 = 55$(种);
$10$级台阶的走法有$55 + 34 = 89$(种)。
答案:有$89$种不同的走法。
1. 实验小学大剧场门前共有5级台阶,规定一步只能走一级或两级,那么走过这些台阶一共有多少种不同的方法?
答案:1+4+3=8(种)
【提示】用数组表示不同的走法:(1,1,1,1,1)表示每步只走一级,有1种方法;(2,1,1,1)、(1,2,1,1)、(1,1,2,1)、(1,1,1,2)表示有一步走两级台阶,其他几步都走一级台阶,有4种方法;(2,2,1)、(1,2,2)、(2,1,2)表示有两步各走两级台阶,有一步走一级台阶,有3种方法。因此,走过这些台阶一共有8种不同的方法。
【提示】用数组表示不同的走法:(1,1,1,1,1)表示每步只走一级,有1种方法;(2,1,1,1)、(1,2,1,1)、(1,1,2,1)、(1,1,1,2)表示有一步走两级台阶,其他几步都走一级台阶,有4种方法;(2,2,1)、(1,2,2)、(2,1,2)表示有两步各走两级台阶,有一步走一级台阶,有3种方法。因此,走过这些台阶一共有8种不同的方法。
2. 三位数中,恰好有两个数字相同的数一共有多少个?
答案:9×9+9×9+(9+8×9)=243(个)
【提示】根据题意,符合要求的数可以先分成三类:百位和十位相同;百位和个位相同;十位和个位相同。百位和十位是“11”的有9个:110,112,113,…,119,同样地,百位和十位是“22”的有9个,…,百位和十位是“99”的有9个;百位和个位是“11”的有9个,同样地,百位和个位是“22”的有9个,…,百位和个位是“99”的有9个;十位和个位是“00”的有9个,十位和个位是“11”的有8个,同样地,十位和个位是“22”的有8个,…,十位和个位是“99”的有8个。因此三位数中,恰好有两个数字相同的数一共有9×9+9×9+(9+8×9)=243(个)。
【提示】根据题意,符合要求的数可以先分成三类:百位和十位相同;百位和个位相同;十位和个位相同。百位和十位是“11”的有9个:110,112,113,…,119,同样地,百位和十位是“22”的有9个,…,百位和十位是“99”的有9个;百位和个位是“11”的有9个,同样地,百位和个位是“22”的有9个,…,百位和个位是“99”的有9个;十位和个位是“00”的有9个,十位和个位是“11”的有8个,同样地,十位和个位是“22”的有8个,…,十位和个位是“99”的有8个。因此三位数中,恰好有两个数字相同的数一共有9×9+9×9+(9+8×9)=243(个)。
3. 1995的各个数位上的数字和是1+9+9+5= 24。那么,在小于2000的四位数中各个数位上的数字和等于24的数共有多少个?
答案:1+2+3+4+5=15(个)
【提示】小于2000的四位数,千位数字是1,要使数字和为24,只需其余三位数字的和是23。因为十位、个位数字的和最多为9+9=18,因此,百位数字至少是5。,分类如下:①百位为5时,有1599一个;②百位为6时,有1689、1698两个;③百位为7时,有1779、1788、1797三个;④百位为8时,有1869、1878、1887、1896四个;⑤百位为9时,有1959、1968、1977、1986、1995五个。因此小于2000的四位数中各位数字和等于24的数共有1+2+3+4+5=15(个)。
【提示】小于2000的四位数,千位数字是1,要使数字和为24,只需其余三位数字的和是23。因为十位、个位数字的和最多为9+9=18,因此,百位数字至少是5。,分类如下:①百位为5时,有1599一个;②百位为6时,有1689、1698两个;③百位为7时,有1779、1788、1797三个;④百位为8时,有1869、1878、1887、1896四个;⑤百位为9时,有1959、1968、1977、1986、1995五个。因此小于2000的四位数中各位数字和等于24的数共有1+2+3+4+5=15(个)。
4. 一位农民1月份买了一对刚出生的小兔,1个月后,这对小兔长成了大兔;1个月后,又生下一对小兔。照这样下去,12月份,他家一共有多少只兔子?
答案:兔子对数规律为1、1、2、3、5、8、13、21、34、55、89、144。所以,12月份(即11个月后)就变成了144对兔子,共144×2=288(只)。
【提示】初始是1对小兔,1个月后是1对大兔,2个月后是1对大兔+1对小兔;3个月后是2对大兔+1对小兔;4个月后是3对大兔+2对小兔……兔子每个月的对数为1、1、2、3、5、8、13、21、34、55、89、144。所以12月份(即11个月后)就变成了144对兔子,共144×2=288(只)。
【提示】初始是1对小兔,1个月后是1对大兔,2个月后是1对大兔+1对小兔;3个月后是2对大兔+1对小兔;4个月后是3对大兔+2对小兔……兔子每个月的对数为1、1、2、3、5、8、13、21、34、55、89、144。所以12月份(即11个月后)就变成了144对兔子,共144×2=288(只)。
5. 小悦买了10块巧克力,她每天最少吃一块,最多吃3块,直到吃完,共有多少种吃法?
答案:274种 【提示】递推法。吃1块只有1种吃法;吃2块有1+1和2两种吃法;吃3块有1+1+1,1+2,2+1,3共4种吃法;吃4块有1+1+1+1,1+1+2,1+2+1,2+1+1,2+2,1+3,3+1共7种吃法;吃5块有2+4+7=13(种)吃法;吃6块有4+7+13=24(种)吃法……依照这一规律,列表写出吃各块(1~10块)时的吃法数如下。最后递推得到吃10块巧克力有274种吃法。
块数 1 2 3 4 5 6 7 8 9 10
吃法 1 2 4 7 13 24 44 81 149 274
块数 1 2 3 4 5 6 7 8 9 10
吃法 1 2 4 7 13 24 44 81 149 274