1. 一张靶纸共三圈,投中内圈得 10 环,其余依次是 8 环、6 环。小乐投中三次,得的环数有(
A.5
B.6
C.7
D.8
C
)种可能。A.5
B.6
C.7
D.8
答案:C 【提示】分别是18、20、22、24、26、28、30。
2. 某信号兵用红、黄、蓝 3 面旗从上到下挂在旗杆上的三个位置表示不同的信号。每次可以挂 1 面、2 面或 3 面,并且不同的顺序表示不同的信号。一共可以表示出多少种不同的信号?
答案:15种 【提示】只挂一面有3种;只挂两面有6种;挂三面有6种。所以一共有3+6+6=15(种)。
解析:
挂1面旗:3种
挂2面旗:$3×2=6$种
挂3面旗:$3×2×1=6$种
总信号数:$3+6+6=15$种
答:一共可以表示出15种不同的信号。
挂2面旗:$3×2=6$种
挂3面旗:$3×2×1=6$种
总信号数:$3+6+6=15$种
答:一共可以表示出15种不同的信号。
3. 编号为 1、2、3、4、5、6 的六位运动员进行乒乓球单循环赛。到现在为止,编号为 1、2、3、4、5 的运动员已参加比赛的场数正好分别等于他们的编号数,编号为 6 的运动员已经赛了几场?
答案:
编号为6的运动员已经赛了3场。【提示】如图所示: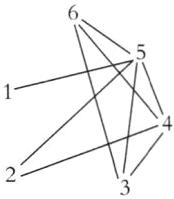
编号为6的运动员已经赛了3场。【提示】如图所示:

4. 两人按自然数顺序轮流报数,每人只能报 1 个或 2 个数。比如第 1 个人可以报 1,第 2 个人可以报 2 或 2、3;第 1 个人也可以报 1、2,第 2 个人可以报 3 或 3、4。这样继续下去,谁报到 30,谁就胜。谁有必胜的策略?
答案:后报数者有必胜的策略。【提示】倒推法,从后面往前想,假如我报数为29,那么对方报一个数就可把30抢走了;如果我报28,那么对方报29、30也把30抢走了。所以,要想抢30,必须先抢27;同样,要抢27,必须先抢24;要抢24,必须先抢21;以此类推:21、18、15、12、9、6、3,第一步必须抢3,后报数的人一定能先抢到3。
解析:
后报数者有必胜的策略。
要抢到30,需先抢到27;要抢到27,需先抢到24;依次类推,需抢到21、18、15、12、9、6、3。
后报数者可根据先报数者的报数,保证每轮两人共报3个数(对方报1个数则自己报2个数,对方报2个数则自己报1个数),从而依次抢到3、6、9、…、30。
因此,后报数者必胜。
要抢到30,需先抢到27;要抢到27,需先抢到24;依次类推,需抢到21、18、15、12、9、6、3。
后报数者可根据先报数者的报数,保证每轮两人共报3个数(对方报1个数则自己报2个数,对方报2个数则自己报1个数),从而依次抢到3、6、9、…、30。
因此,后报数者必胜。
5. 甲、乙两人抓棋子,规定最多抓 3 枚,最少抓 1 枚,谁抓得最后 1 枚棋子就算输。若甲先抓,棋子数为 2001 枚,则乙是否有必胜的策略?
答案:有 【提示】由2001=500×(3+1)+1知,乙有必胜策略:乙取的枚数始终保持与甲取的枚数之和为4。双方各取500次后,剩1枚,甲不得不拿走最后1枚,甲必输。
解析:
乙有必胜策略。
因为 $2001 = 500 × (3+1) + 1$,乙取的枚数始终保持与甲取的枚数之和为4。双方各取500次后,剩余1枚,甲需取走最后1枚,甲输。
结论:乙有必胜策略。
因为 $2001 = 500 × (3+1) + 1$,乙取的枚数始终保持与甲取的枚数之和为4。双方各取500次后,剩余1枚,甲需取走最后1枚,甲输。
结论:乙有必胜策略。
6. 下图中有 12 个格子,棋子初始在第 1 格,甲、乙两人轮流移动棋子,每次至少向前移 1 格或 2 格,谁将棋子移到最后一格,谁就胜利。让乙先移动,甲如何获得胜利?(写出一种移法即可)
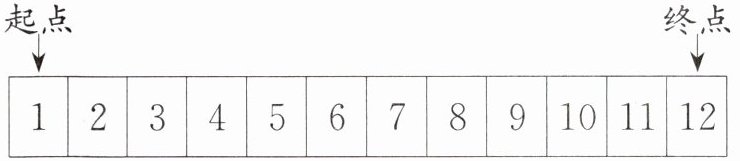

答案:乙移动1格时,甲移动2格;乙移动2格时,甲移动1格,确保与乙每次移动共3格,最后甲移动最后一格。【提示】12是3的倍数。