(1)在第n个图形中,每一横行共有
(2)在铺设的第n个图形中,共有多少块瓷砖?
(3)如果每块灰瓷砖4元,每块白瓷砖3元,那么铺设第10个图形时,共需花多少钱购买瓷砖?
n+3
块瓷砖,每一竖列共有n+2
块瓷砖。(2)在铺设的第n个图形中,共有多少块瓷砖?
(n+3)(n+2)
(3)如果每块灰瓷砖4元,每块白瓷砖3元,那么铺设第10个图形时,共需花多少钱购买瓷砖?
514元
答案:解析:
(1)观察图形可知,在第n个图形中,每一横行共有$n + 3$块瓷砖,每一竖列共有$n + 2$块瓷砖。
(2)根据长方形面积公式,可得第n个图形中瓷砖总数为$(n + 3)(n + 2)$块。
(3)当$n = 10$时,横行瓷砖数为$n+3 = 13$块,竖列瓷砖数为$n + 2 = 12$块,则瓷砖总数为$(10 + 3)×(10 + 2)=13×12 = 156$块。
白瓷砖:白瓷砖组成的长方形长为$n + 1$,宽为$n$,当$n = 10$时,白瓷砖数量为$10×(10 + 1)=110$块。
灰瓷砖:灰瓷砖数量等于瓷砖总数减去白瓷砖数量,即$156 - 110 = 46$块。
费用:已知每块灰瓷砖$4$元,每块白瓷砖$3$元,则总费用为$46×4 + 110×3=184+330 = 514$元。
答案:
(1)$n + 3$;$n + 2$
(2)$(n + 3)(n + 2)$
(3)共需花$514$元购买瓷砖。
(1)观察图形可知,在第n个图形中,每一横行共有$n + 3$块瓷砖,每一竖列共有$n + 2$块瓷砖。
(2)根据长方形面积公式,可得第n个图形中瓷砖总数为$(n + 3)(n + 2)$块。
(3)当$n = 10$时,横行瓷砖数为$n+3 = 13$块,竖列瓷砖数为$n + 2 = 12$块,则瓷砖总数为$(10 + 3)×(10 + 2)=13×12 = 156$块。
白瓷砖:白瓷砖组成的长方形长为$n + 1$,宽为$n$,当$n = 10$时,白瓷砖数量为$10×(10 + 1)=110$块。
灰瓷砖:灰瓷砖数量等于瓷砖总数减去白瓷砖数量,即$156 - 110 = 46$块。
费用:已知每块灰瓷砖$4$元,每块白瓷砖$3$元,则总费用为$46×4 + 110×3=184+330 = 514$元。
答案:
(1)$n + 3$;$n + 2$
(2)$(n + 3)(n + 2)$
(3)共需花$514$元购买瓷砖。
1. 古希腊的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”,把1、4、9、16……这样的数称为“正方形数”。从下图中可以发现:任何一个大于1的“正方形数”都可以写成两个相邻“三角形数”的和。下面的等式中,符合这一规律的是(
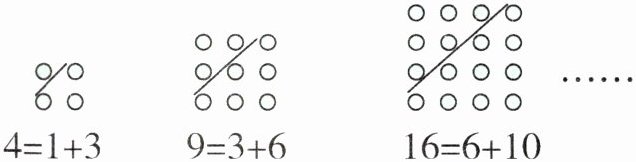
A.25= 9+16
B.36= 15+21
C.49= 18+31
D.64= 31+33
B
)。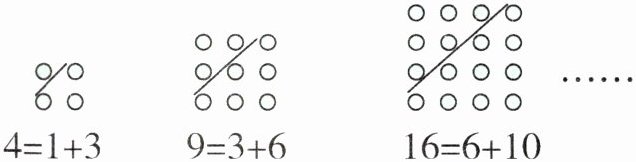
A.25= 9+16
B.36= 15+21
C.49= 18+31
D.64= 31+33
答案:1.B 【提示】三角形数从1开始,第几个三角形数就是从1开始的连续自然数相加到几,正方形数也就是平方数,将三角形数接着写下去,依次为1、3、6、10、15、21、28、36。观察选项,只有B符合,其他选项中均不是“三角形数”。
2. 如右下图,先将一张正方形纸片剪成4个小正方形,然后将其中的一个正方形再剪成4个小正方形,接着将其中的一个小正方形剪成4个更小的正方形,如此继续下去。根据以上操作方法,操作n次后会有多少个正方形?


答案:2.(3n+1)个 【提示】操作一次可得到4个正方形;操作两次可得到4+3=7(个)正方形;操作三次可得到4+2×3=10(个)正方形;…;操作n次可得到[4+(n-1)×3]个正方形,(3n+1)个正方形。
解析:
操作1次:4个
操作2次:4+3=7个
操作3次:4+3×2=10个
...
操作n次:$4 + 3(n - 1) = 3n + 1$个
答:操作n次后会有$(3n + 1)$个正方形。
操作2次:4+3=7个
操作3次:4+3×2=10个
...
操作n次:$4 + 3(n - 1) = 3n + 1$个
答:操作n次后会有$(3n + 1)$个正方形。
3. 请仔细观察下面的直角三角形,根据正方形的个数与直角三角形个数的关系把下表填写完整。




12
26
4(n-1)(或4n-4)
答案:3.12 26 4(n-1)(或4n-4)
解析:
12 26 $4(n-1)$