1. 建设新农村,倡导新生活。如下图为某村庄的一个长方形广场,四角都有一块边长为x m的正方形草地,长方形的长为a m,宽为b m。
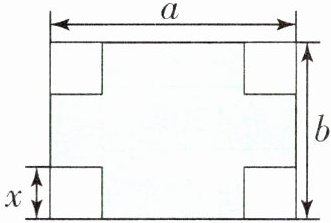
(1)请用式子表示出涂色部分的面积。
(2)若长方形广场的长为450 m,宽为200 m,正方形的边长为10 m,则求涂色部分的面积。
(1)请用式子表示出涂色部分的面积。
(2)若长方形广场的长为450 m,宽为200 m,正方形的边长为10 m,则求涂色部分的面积。
答案：1.
(1)$(ab - 4x^{2})$
【提示】涂色部分面积=长方形的面积 - 4个正方形的面积和
(2)$450×200 - 4×10^{2}=89600(m^{2})$
【提示】把对应数值代入式子中,求出最后的结果即可。
(1)$(ab - 4x^{2})$
【提示】涂色部分面积=长方形的面积 - 4个正方形的面积和
(2)$450×200 - 4×10^{2}=89600(m^{2})$
【提示】把对应数值代入式子中,求出最后的结果即可。
2. 下面的图都是由相同的小正方形按照一定的规律摆放而成的,其中第1个图中共有3个小正方形,第2个图中共有8个小正方形,第3个图中共有15个小正方形,第4个图中共有24个小正方形……
(1)照此规律摆放下去,第n个图中有(
(2)当n= 64时,一共有多少个小正方形？
(1)照此规律摆放下去,第n个图中有(
n²+2n
)个小正方形。(用含n的式子表示)(2)当n= 64时,一共有多少个小正方形？
当n=64时，n²+2n=64²+2×64=4224
答案：2.
(1)$n^{2}+2n$【提示】第1个图中小正方形的个数$3=1×1 + 2×1$,第2个图中小正方形的个数$8=2×2 + 2×2$,第3个图中小正方形的个数$15=3×3 + 2×3$,第4个图中小正方形的个数$24=4×4 + 2×4,... $,所以第n个图中小正方形的个数为$n^{2}+2n$。
(2)当$n=64$时,$n^{2}+2n=64^{2}+2×64=4224$【提示】将$n=64$代入
(1)中的关系式计算即可。
(1)$n^{2}+2n$【提示】第1个图中小正方形的个数$3=1×1 + 2×1$,第2个图中小正方形的个数$8=2×2 + 2×2$,第3个图中小正方形的个数$15=3×3 + 2×3$,第4个图中小正方形的个数$24=4×4 + 2×4,... $,所以第n个图中小正方形的个数为$n^{2}+2n$。
(2)当$n=64$时,$n^{2}+2n=64^{2}+2×64=4224$【提示】将$n=64$代入
(1)中的关系式计算即可。
3. 对于数a、b,定义运算“▽”为a▽b= (a+3)×(b-5),计算5▽(6▽7)的值。
答案：$6▽7=(6+3)×(7 - 5)=18$$5▽(6▽7)=5▽18=(5+3)×(18 - 5)=104$【提示】由题可知,$a▽b=(a+3)×(b - 5)$表示一种新运算,把$a=6,b=7$代入算式可求得$6▽7$的结果是18,同理可求得$5▽18$的结果。
解析：
$6▽7=(6+3)×(7 - 5)=9×2=18$
$5▽(6▽7)=5▽18=(5+3)×(18 - 5)=8×13=104$
$5▽(6▽7)=5▽18=(5+3)×(18 - 5)=8×13=104$
4. 对任意的数a、b,定义：f(a)= 2a+1,g(b)= b×b。
(1)求f(5)-g(3)的值。
(2)求f(g(2))+g(f(2))的值。
(1)求f(5)-g(3)的值。
(2)求f(g(2))+g(f(2))的值。
答案：
(1)$f(5)=2×5 + 1=11$$g(3)=3×3=9$$f(5)-g(3)=11 - 9=2$
(2)$g(2)=2×2=4$$f(g(2))=f(4)=2×4 + 1=9$$f(2)=2×2 + 1=5$$g(f(2))=g(5)=5×5=25$$f(g(2))+g(f(2))=9 + 25=34$【提示】按照新运算的定义,$f(a)$就是这个数的2倍与1的和;$g(b)$就是这个数的平方。在进行新运算时,有括号的,要先算括号里面的。
(1)$f(5)=2×5 + 1=11$$g(3)=3×3=9$$f(5)-g(3)=11 - 9=2$
(2)$g(2)=2×2=4$$f(g(2))=f(4)=2×4 + 1=9$$f(2)=2×2 + 1=5$$g(f(2))=g(5)=5×5=25$$f(g(2))+g(f(2))=9 + 25=34$【提示】按照新运算的定义,$f(a)$就是这个数的2倍与1的和;$g(b)$就是这个数的平方。在进行新运算时,有括号的,要先算括号里面的。