(1)在括号里填上合适的数。
28500 平方米= (
0.24 平方千米= (
7 公顷 40 平方米= (
0.4 公顷= (
209 公顷= (
3.06 平方千米= (
28500 平方米= (
2.85
)公顷0.24 平方千米= (
24
)公顷7 公顷 40 平方米= (
7.004
)公顷0.4 公顷= (
4000
)平方米209 公顷= (
2
)平方千米(9
)公顷3.06 平方千米= (
3
)平方千米 (6
)公顷答案:
(1)2.85 24 7.004 4000 2 9 3 6 【提示】高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率。
(1)2.85 24 7.004 4000 2 9 3 6 【提示】高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率。
解析:
2.85 24 7.004 4000 2 9 3 6
(2)如果一个直角三角形的三条边长分别为 3 cm、4 cm 和 5 cm,那么这个直角三角形斜边上的高是(
2.4
)cm。答案:
(2)2.4
(2)2.4
解析:
这个直角三角形的面积为$\frac{1}{2} × 3 × 4 = 6\,\text{cm}^2$。设斜边上的高为$h\,\text{cm}$,根据面积公式可得$\frac{1}{2} × 5 × h = 6$,解得$h = \frac{12}{5} = 2.4$。
2.4
2.4
(3)一个直角梯形的上底是 6 分米,下底是 12 分米,两条腰分别是 8 分米和 10 分米。从这个梯形中减去一个最大的三角形,剩下部分的面积是(
24
)平方分米。答案:
(3)24
(3)24
解析:
直角梯形的高为较短的腰,即8分米。
梯形面积:$\frac{(6+12)×8}{2}=72$平方分米。
最大三角形面积:$\frac{12×8}{2}=48$平方分米。
剩下部分面积:$72-48=24$平方分米。
24
梯形面积:$\frac{(6+12)×8}{2}=72$平方分米。
最大三角形面积:$\frac{12×8}{2}=48$平方分米。
剩下部分面积:$72-48=24$平方分米。
24
(4)已知平行四边形的两条邻边的长分别是 5 厘米和 8 厘米,其中一条边上的高是 6 厘米,则另一条边上的高是(
3.75
)厘米。若平行四边形的两条高的长分别是 5 分米和 8 分米,其中一条高对应的底长 7 分米,则这个平行四边形的面积是(56
)平方分米。答案:
(4)3.75 56
易错警示
高和底对应
平行四边形中有两个不一样的高和一个底,根据题意先画图,再根据直角三角形斜边大于直角边进行判断。
(4)3.75 56
易错警示
高和底对应
平行四边形中有两个不一样的高和一个底,根据题意先画图,再根据直角三角形斜边大于直角边进行判断。
(5)钉子板上每相邻两枚钉子之间的距离都是 1 厘米,一个不规则图形的边上一共有 10 枚钉子,且内部有 3 枚钉子,该图形的面积是(
7
)平方厘米。答案:
(5)7 【提示】通过画图可知,当多边形的边上一共有10枚钉子时,面积是10÷2+3-1=7(平方厘米)。
(5)7 【提示】通过画图可知,当多边形的边上一共有10枚钉子时,面积是10÷2+3-1=7(平方厘米)。
解析:
根据毕克定理,图形面积$S = I+\frac{B}{2}-1$(其中$I$为内部钉子数,$B$为边上钉子数)。已知$I = 3$,$B=10$,则$S=3+\frac{10}{2}-1=3 + 5-1=7$。
7
7
(6)一张长方形彩纸,长是 40 厘米,宽是 25 厘米,把它剪成两条直角边都是 10 厘米长的直角三角形小旗,最多能剪
16
面(不能拼接)。答案:
(6)16 【提示】把两个直角三角形拼成一个正方形,然后看长方形的长和宽分别包含多少个正方形的边长:40÷10=4(个),25÷10≈2(个),一共能剪4×2×2=16(面)直角三角形小旗。
(6)16 【提示】把两个直角三角形拼成一个正方形,然后看长方形的长和宽分别包含多少个正方形的边长:40÷10=4(个),25÷10≈2(个),一共能剪4×2×2=16(面)直角三角形小旗。
解析:
40÷10=4(个)
25÷10≈2(个)
4×2×2=16(面)
16
25÷10≈2(个)
4×2×2=16(面)
16
(7)如图,在直角三角形 ABC 中,涂色部分的面积是 12 平方厘米,D、E 分别是 BC、AC 的中点,则三角形 ABC 的面积是(
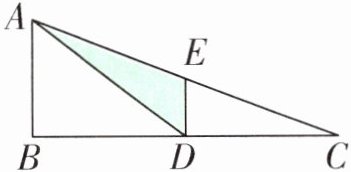
48
)平方厘米。
答案:
(7)48 【提示】由D、E 分别是BC、AC 的中点,可知涂色部分的面积占三角形 ABC 面积的$\frac{1}{4}$,可以求出三角形 ABC 的面积是12×4=48(平方厘米)。
(7)48 【提示】由D、E 分别是BC、AC 的中点,可知涂色部分的面积占三角形 ABC 面积的$\frac{1}{4}$,可以求出三角形 ABC 的面积是12×4=48(平方厘米)。
2. 王爷爷在一块三角形菜地上全部种大白菜,底是 10.4 米,对应的高是 8 米。
(1)如果每平方米菜地需要 0.4 千克化肥,那么王爷爷准备 16 千克化肥够吗?
(2)如果每棵大白菜需占地 20 平方分米,那么这块菜地一共可以种多少棵大白菜?
(1)如果每平方米菜地需要 0.4 千克化肥,那么王爷爷准备 16 千克化肥够吗?
(2)如果每棵大白菜需占地 20 平方分米,那么这块菜地一共可以种多少棵大白菜?
答案:
(1)10.4×8÷2=41.6(平方米)
41.6×0.4=16.64(千克)
16.64>16,不够。
(2)41.6平方米=4160平方分米
4160÷20=208(棵)
【提示】先求出三角形菜地的面积,再用总面积÷每棵大白菜的占地面积。
(1)10.4×8÷2=41.6(平方米)
41.6×0.4=16.64(千克)
16.64>16,不够。
(2)41.6平方米=4160平方分米
4160÷20=208(棵)
【提示】先求出三角形菜地的面积,再用总面积÷每棵大白菜的占地面积。
(1)一个梯形的上底与下底的和与梯形的高相等。如果上底与下底的和减去 3 厘米,梯形的高增加 3 厘米,那么现在梯形的面积与原来相比,(
A.变大了
B.变小了
C.不变
D.无法确定
B
)。A.变大了
B.变小了
C.不变
D.无法确定
答案:
(1)B
(1)B
解析:
设原来梯形上底与下底的和为$a$厘米,则原来梯形的高为$a$厘米,原来梯形面积为$\frac{1}{2}a \cdot a=\frac{1}{2}a^{2}$平方厘米。
变化后上底与下底的和为$(a - 3)$厘米,高为$(a + 3)$厘米,现在梯形面积为$\frac{1}{2}(a - 3)(a + 3)=\frac{1}{2}(a^{2}-9)=\frac{1}{2}a^{2}-\frac{9}{2}$平方厘米。
因为$\frac{1}{2}a^{2}-\frac{9}{2} < \frac{1}{2}a^{2}$,所以现在梯形的面积与原来相比变小了。
B
变化后上底与下底的和为$(a - 3)$厘米,高为$(a + 3)$厘米,现在梯形面积为$\frac{1}{2}(a - 3)(a + 3)=\frac{1}{2}(a^{2}-9)=\frac{1}{2}a^{2}-\frac{9}{2}$平方厘米。
因为$\frac{1}{2}a^{2}-\frac{9}{2} < \frac{1}{2}a^{2}$,所以现在梯形的面积与原来相比变小了。
B
(2)下面说法中,正确的有(
①两个等底等高的三角形,一定能拼成一个平行四边形。
②两个面积相等的三角形,它们的底和高都相等。
③一个平行四边形的面积是与它等底等高的三角形面积的 2 倍,一个三角形的面积是与它等底等高的平行四边形面积的一半。
④三角形的底扩大到原来的 3 倍,高缩小到原来的$\frac {1}{3}$,三角形的面积不变。
A.1
B.2
C.3
D.4
B
)个。①两个等底等高的三角形,一定能拼成一个平行四边形。
②两个面积相等的三角形,它们的底和高都相等。
③一个平行四边形的面积是与它等底等高的三角形面积的 2 倍,一个三角形的面积是与它等底等高的平行四边形面积的一半。
④三角形的底扩大到原来的 3 倍,高缩小到原来的$\frac {1}{3}$,三角形的面积不变。
A.1
B.2
C.3
D.4
答案:
(2)B
(2)B
解析:
①两个等底等高的三角形,形状不一定相同,不一定能拼成一个平行四边形,错误;
②两个面积相等的三角形,底和高的乘积相等,但底和高不一定都相等,错误;
③平行四边形面积公式为$S = 底×高$,三角形面积公式为$S = \frac{1}{2}×底×高$,所以一个平行四边形的面积是与它等底等高的三角形面积的2倍,一个三角形的面积是与它等底等高的平行四边形面积的一半,正确;
④原三角形面积$S = \frac{1}{2}×底×高$,变化后面积$S' = \frac{1}{2}×(3×底)×(\frac{1}{3}×高) = \frac{1}{2}×底×高 = S$,面积不变,正确。
正确的有2个。
B
②两个面积相等的三角形,底和高的乘积相等,但底和高不一定都相等,错误;
③平行四边形面积公式为$S = 底×高$,三角形面积公式为$S = \frac{1}{2}×底×高$,所以一个平行四边形的面积是与它等底等高的三角形面积的2倍,一个三角形的面积是与它等底等高的平行四边形面积的一半,正确;
④原三角形面积$S = \frac{1}{2}×底×高$,变化后面积$S' = \frac{1}{2}×(3×底)×(\frac{1}{3}×高) = \frac{1}{2}×底×高 = S$,面积不变,正确。
正确的有2个。
B