(1)正方体的棱长扩大为原来的3倍,棱长之和扩大为原来的
3
倍,表面积扩大为原来的9
倍,体积扩大为原来的27
倍。答案:3 9 27 【提示】可以假设原来正方体的棱长是1厘米,棱长扩大为原来的3倍后是3厘米,分别计算出原来和现在的正方体的棱长和、表面积和体积后进行比较即可得到结论。
解析:
假设原来正方体的棱长是1厘米。
棱长之和:原来 $12×1 = 12$ 厘米,扩大后 $12×3 = 36$ 厘米,$36÷12 = 3$ 倍。
表面积:原来 $6×1^2 = 6$ 平方厘米,扩大后 $6×3^2 = 54$ 平方厘米,$54÷6 = 9$ 倍。
体积:原来 $1^3 = 1$ 立方厘米,扩大后 $3^3 = 27$ 立方厘米,$27÷1 = 27$ 倍。
3 9 27
棱长之和:原来 $12×1 = 12$ 厘米,扩大后 $12×3 = 36$ 厘米,$36÷12 = 3$ 倍。
表面积:原来 $6×1^2 = 6$ 平方厘米,扩大后 $6×3^2 = 54$ 平方厘米,$54÷6 = 9$ 倍。
体积:原来 $1^3 = 1$ 立方厘米,扩大后 $3^3 = 27$ 立方厘米,$27÷1 = 27$ 倍。
3 9 27
(2)新情境冰雪大世界当春日的暖阳散落松花江的冰面,哈尔滨冰雪大世界这座如梦似幻的冰雪城堡便犹如一场盛大而璀璨的梦境,悄然落下帷幕。若哈尔滨冰雪大世界用的冰、雪能融化成25万立方米的水,则这个水量可以装满(
100
)个长50米、宽25米、深20分米的游泳池。答案:100 【提示】20分米=2米,因此游泳池的容积是50×25×2=2500(立方米)。又因为25万立方米=250000立方米,所以这个水量可以装满250000÷2500=100(个)游泳池。
解析:
20分米=2米
游泳池容积:$50×25×2=2500$(立方米)
25万立方米=250000立方米
可装满游泳池个数:$250000÷2500=100$(个)
100
游泳池容积:$50×25×2=2500$(立方米)
25万立方米=250000立方米
可装满游泳池个数:$250000÷2500=100$(个)
100
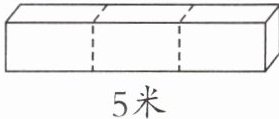
2.把一根长5米的长方体木材截成三段(如
右下图),表面积比原来增加了32平方分米。这根木材的体积是多少立方米?
 思维拓展提优瞄准难维宽度!
思维拓展提优瞄准难维宽度!
右下图),表面积比原来增加了32平方分米。这根木材的体积是多少立方米?
 思维拓展提优瞄准难维宽度!
思维拓展提优瞄准难维宽度!答案:32平方分米=0.32平方米 0.32÷4×5=0.4(立方米) 【提示】木材截成三段,增加了4个横截面的面积,即32平方分米。
解析:
32平方分米=0.32平方米
0.32÷4×5=0.4(立方米)
答:这根木材的体积是0.4立方米。
0.32÷4×5=0.4(立方米)
答:这根木材的体积是0.4立方米。
3. 传统文化卯榫卯(sǔnmǎo)是中国传统建筑、家具及其他器械的主要结构方式,是在两个构件上采用凹凸部位相结合的一种连接方式,凸出部分叫榫(或榫头),凹进部分叫卯(或榫眼、榫槽)。
(1)某榫头从三个方向看到的图形如图所示,该头的体积为(
(2)若要将第(1)题的头补为一个正方体,则至少需要(

(1)某榫头从三个方向看到的图形如图所示,该头的体积为(
14
)cm³。(2)若要将第(1)题的头补为一个正方体,则至少需要(
13
)cm³的木头。
答案:
(1)14 【提示】由题图可得,该榫头可以看作一个3cm×3cm×2cm的长方体去掉四个角(棱长为1cm的正方体)余下的几何体,即3×3×2-1×1×1×4=14(cm³)。
(2)13 【提示】由题意可得,最小的正方体需要的木头为3×3×3=27(cm³),27-14=13(cm³),因此至少需要13cm³的木头。
(1)14 【提示】由题图可得,该榫头可以看作一个3cm×3cm×2cm的长方体去掉四个角(棱长为1cm的正方体)余下的几何体,即3×3×2-1×1×1×4=14(cm³)。
(2)13 【提示】由题意可得,最小的正方体需要的木头为3×3×3=27(cm³),27-14=13(cm³),因此至少需要13cm³的木头。
4.一个长方体容器,长12厘米,宽6厘米,高
8厘米。按右下图这样放置,里面有多少毫
升水?(容器壁厚度忽略不计)

8厘米。按右下图这样放置,里面有多少毫
升水?(容器壁厚度忽略不计)

答案:(12-8+12)×8÷2×6=384(立方厘米) 384立方厘米=384毫升 【提示】先求出上底为12-8=4(厘米)、下底为12厘米、高为8厘米的梯形的面积,再用梯形的面积乘6厘米,即可求出长方体容器里面水的体积。
解析:
梯形上底:$12 - 8 = 4$(厘米)
梯形面积:$\frac{(4 + 12) × 8}{2} = 64$(平方厘米)
水的体积:$64 × 6 = 384$(立方厘米)
$384$立方厘米$= 384$毫升
梯形面积:$\frac{(4 + 12) × 8}{2} = 64$(平方厘米)
水的体积:$64 × 6 = 384$(立方厘米)
$384$立方厘米$= 384$毫升
5.观景台是为观赏景色而搭建的平台。人民
公园在池塘边修建一块长方形的观景台,观
景台的长是40米,如果将72立方米的碎石
平铺在观景台上,那么碎石厚0.3米。这个
观景台的宽是多少米?如果在碎石上浇
0.25米厚的水泥,那么需要多少立方米水泥?
开放探究提优挑战子生!
公园在池塘边修建一块长方形的观景台,观
景台的长是40米,如果将72立方米的碎石
平铺在观景台上,那么碎石厚0.3米。这个
观景台的宽是多少米?如果在碎石上浇
0.25米厚的水泥,那么需要多少立方米水泥?
开放探究提优挑战子生!
答案:72÷0.3÷40=6(米) 40×6×0.25=60(立方米) 【提示】先求出观景台的宽,再根据长方体的体积公式求出水泥的体积。
解析:
观景台的宽:$72÷0.3÷40 = 6$(米)
需要水泥的体积:$40×6×0.25 = 60$(立方米)
需要水泥的体积:$40×6×0.25 = 60$(立方米)
6.把一个长方体分割成一个表面积是150平
方厘米的正方体和一个表面积是110平方
厘米的长方体。原长方体的体积是多少立
方厘米?
方厘米的正方体和一个表面积是110平方
厘米的长方体。原长方体的体积是多少立
方厘米?
答案:150÷6=25(平方厘米) 25=5×5,故正方体的棱长为5厘米。 (110-25×2)÷4=15(平方厘米) 15÷5=3(厘米) 5+3=8(厘米) 25×8=200(立方厘米) 【提示】这个长方体有两个相对的面是正方形,可以根据正方体的表面积求出正方体的棱长。
解析:
150÷6=25(平方厘米)
25=5×5,正方体棱长为5厘米。
(110-25×2)÷4=15(平方厘米)
15÷5=3(厘米)
5+3=8(厘米)
25×8=200(立方厘米)
答:原长方体的体积是200立方厘米。
25=5×5,正方体棱长为5厘米。
(110-25×2)÷4=15(平方厘米)
15÷5=3(厘米)
5+3=8(厘米)
25×8=200(立方厘米)
答:原长方体的体积是200立方厘米。