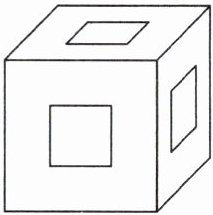
例 如图,在一个棱长为10厘米的正方体的上面、右面、前面的中心位置分别挖一个开口为边长4厘米的正方形小孔,直至对面,做成一个模型。求这个模型的体积和表面积。
解析
模型的体积等于正方体的体积减去挖去部分的体积。模型的表面积是原来正方体的表面积减去六个边长为4厘米的正方形的面积,再加上三个高为(10-4)厘米、长和宽都是4厘米的长方体的侧面积。
答案:
体积:$10×10×10-4×4×10×3+4×4×4×2= 648$(立方厘米)
表面积:$10×10×6-4×4×6+4×(10-4)×4×3= 792$(平方厘米)
答:这个模型的体积是648立方厘米,表面积是792平方厘米。

解析
模型的体积等于正方体的体积减去挖去部分的体积。模型的表面积是原来正方体的表面积减去六个边长为4厘米的正方形的面积,再加上三个高为(10-4)厘米、长和宽都是4厘米的长方体的侧面积。
答案:
体积:$10×10×10-4×4×10×3+4×4×4×2= 648$(立方厘米)
表面积:$10×10×6-4×4×6+4×(10-4)×4×3= 792$(平方厘米)
答:这个模型的体积是648立方厘米,表面积是792平方厘米。
答案:解析:
模型的体积等于正方体的体积减去挖去部分的体积,而挖去部分的体积等于三个小长方体的体积减去重叠部分(两个小正方体)的体积。
模型的表面积是原来正方体的表面积减去六个边长为4厘米的正方形的面积,再加上三个高为$(10-4)$厘米、长和宽都是4厘米的长方体的侧面积。
答案:
体积:
$10×10×10 - [4×4×(10+10-4)+4×4×4×2]=648$(立方厘米),
表面积:
$10×10×6 - 4×4×6 + 4×(10 - 4)×4×3 =792$(平方厘米),
答:这个模型的体积是648立方厘米,表面积是792平方厘米。
模型的体积等于正方体的体积减去挖去部分的体积,而挖去部分的体积等于三个小长方体的体积减去重叠部分(两个小正方体)的体积。
模型的表面积是原来正方体的表面积减去六个边长为4厘米的正方形的面积,再加上三个高为$(10-4)$厘米、长和宽都是4厘米的长方体的侧面积。
答案:
体积:
$10×10×10 - [4×4×(10+10-4)+4×4×4×2]=648$(立方厘米),
表面积:
$10×10×6 - 4×4×6 + 4×(10 - 4)×4×3 =792$(平方厘米),
答:这个模型的体积是648立方厘米,表面积是792平方厘米。
1. 在一个棱长为6cm的正方体的上面正中间挖去一个棱长为2cm的小正方体(如图所示)。求所得立体图形的表面积。


答案:解析:本题考查正方体的表面积。
大正方体的棱长为$6cm$,小正方体的棱长为$2cm$。
大正方体的一个面的面积为$6 × 6 = 36({cm}^{2})$。
大正方体的表面积为$6 × 36 = 216({cm}^{2})$。
小正方体一个面的面积为$2 × 2 = 4({cm}^{2})$。
小正方体有4个面暴露在外(上面、前面、后面、左面、右面中的四个),
所以新增的表面积为$4 × 4 = 16({cm}^{2})$,
但是小正方体的底面(即与大正方体接触的那个面)不计入总表面积,
因为它在大正方体内部。
所得立体图形的表面积为大正方体的表面积加上小正方体新增的表面积,
即$216 + 16 = 232({cm}^{2})$。
答案:$232{cm}^{2}$。
大正方体的棱长为$6cm$,小正方体的棱长为$2cm$。
大正方体的一个面的面积为$6 × 6 = 36({cm}^{2})$。
大正方体的表面积为$6 × 36 = 216({cm}^{2})$。
小正方体一个面的面积为$2 × 2 = 4({cm}^{2})$。
小正方体有4个面暴露在外(上面、前面、后面、左面、右面中的四个),
所以新增的表面积为$4 × 4 = 16({cm}^{2})$,
但是小正方体的底面(即与大正方体接触的那个面)不计入总表面积,
因为它在大正方体内部。
所得立体图形的表面积为大正方体的表面积加上小正方体新增的表面积,
即$216 + 16 = 232({cm}^{2})$。
答案:$232{cm}^{2}$。
2. 在一个长、宽、高分别是8厘米、6厘米、5厘米的长方体的8个顶点处,分别截下一个棱长为1厘米的小正方体后,剩下立体图形的表面积是多少平方厘米? 体积是多少立方厘米?
答案:表面积:
原长方体表面积:$(8×6 + 8×5 + 6×5)×2 = (48 + 40 + 30)×2 = 118×2 = 236$(平方厘米)
截去小正方体后表面积不变,仍为236平方厘米。
体积:
原长方体体积:$8×6×5 = 240$(立方厘米)
截去小正方体总体积:$1×1×1×8 = 8$(立方厘米)
剩下立体图形体积:$240 - 8 = 232$(立方厘米)
答:剩下立体图形的表面积是236平方厘米,体积是232立方厘米。
原长方体表面积:$(8×6 + 8×5 + 6×5)×2 = (48 + 40 + 30)×2 = 118×2 = 236$(平方厘米)
截去小正方体后表面积不变,仍为236平方厘米。
体积:
原长方体体积:$8×6×5 = 240$(立方厘米)
截去小正方体总体积:$1×1×1×8 = 8$(立方厘米)
剩下立体图形体积:$240 - 8 = 232$(立方厘米)
答:剩下立体图形的表面积是236平方厘米,体积是232立方厘米。
3. 有一个棱长为4cm的正方体,从它的右上方截去一个长、宽、高分别为4cm、2cm、1cm的长方体(如图),求剩下部分的表面积。


答案:原正方体表面积:$4×4×6 = 96$($cm^2$)
截去长方体后,减少的表面积:$2×1×2 = 4$($cm^2$)
剩下部分表面积:$96 - 4 = 92$($cm^2$)
答:剩下部分的表面积是$92cm^2$。
截去长方体后,减少的表面积:$2×1×2 = 4$($cm^2$)
剩下部分表面积:$96 - 4 = 92$($cm^2$)
答:剩下部分的表面积是$92cm^2$。
4. 一块棱长为6厘米的正方体木料,如果在前面、上面、右面的中心各向后挖一个口为边长2厘米的正方形孔,直至对面,那么剩余木料的体积是多少?
答案:【提示】可以先计算三条孔道的体积,因为三条孔道相交的地方是一个正方体,且这个正方体总共被计算了3次,实际只计算1次就可以,因此三条孔道的实际总体积为三条孔道的体积减去2个正方体的体积;然后用原来正方体的体积减去三条孔道的实际总体积即可。
解析:
原来正方体体积:$6×6×6 = 216$(立方厘米)
每条孔道体积:$2×2×6 = 24$(立方厘米),三条孔道体积:$3×24 = 72$(立方厘米)
相交部分为棱长2厘米的正方体,多算次数:$3 - 1 = 2$次,相交部分多算体积:$2×(2×2×2)=16$(立方厘米)
孔道实际总体积:$72 - 16 = 56$(立方厘米)
剩余木料体积:$216 - 56 = 160$(立方厘米)
答:剩余木料的体积是160立方厘米。
每条孔道体积:$2×2×6 = 24$(立方厘米),三条孔道体积:$3×24 = 72$(立方厘米)
相交部分为棱长2厘米的正方体,多算次数:$3 - 1 = 2$次,相交部分多算体积:$2×(2×2×2)=16$(立方厘米)
孔道实际总体积:$72 - 16 = 56$(立方厘米)
剩余木料体积:$216 - 56 = 160$(立方厘米)
答:剩余木料的体积是160立方厘米。