(1)在括号里写出下面各数的倒数。
$\frac{4}{5}$(
3(
我发现:(a 是大于 0 的数)
当$a>1$时:$\frac{1}{a}$
当$a<1$时:$\frac{1}{a}$
$\frac{4}{5}$(
$\frac{5}{4}$
) $\frac{13}{9}$($\frac{9}{13}$
) $\frac{1}{10}$(10
)3(
$\frac{1}{3}$
) 0.5(2
) $\frac{11}{10}$($\frac{10}{11}$
)我发现:(a 是大于 0 的数)
当$a>1$时:$\frac{1}{a}$
<
1;当$a= 1$时:$\frac{1}{a}$=
1;当$a<1$时:$\frac{1}{a}$
>
1。答案:1.
(1)$\frac {5}{4}$ $\frac {9}{13}$ 10 $\frac {1}{3}$ 2 $\frac {10}{11}$
< = >
【提示】乘积是1的两个数互为倒数。1的倒数是1,0没有倒数。
(1)$\frac {5}{4}$ $\frac {9}{13}$ 10 $\frac {1}{3}$ 2 $\frac {10}{11}$
< = >
【提示】乘积是1的两个数互为倒数。1的倒数是1,0没有倒数。
(2)已知a和b互为倒数,则$\frac{8}{a}×\frac{8}{b}$的计算结果是(
64
)。答案:1.
(2)64 【提示】$\frac {8}{a}×\frac {8}{b}=\frac {64}{ab}$,因为a和b互为倒数,所以$ab=1,\frac {64}{ab}=64$。
(2)64 【提示】$\frac {8}{a}×\frac {8}{b}=\frac {64}{ab}$,因为a和b互为倒数,所以$ab=1,\frac {64}{ab}=64$。
(1)a与$\frac{1}{a}$互为倒数的条件是(
A.a 是整数
B.a 是自然数
C.a 不等于0
D.$a= 1$
C
)。A.a 是整数
B.a 是自然数
C.a 不等于0
D.$a= 1$
答案:2.
(1)C 【提示】因为分数的分母不能为0,所以a不等于0。
(1)C 【提示】因为分数的分母不能为0,所以a不等于0。
(2)若甲数的倒数大于乙数的倒数,则甲数和乙数相比,(
A.甲数大
B.乙数大
C.一样大
D.无法比较
B
)。A.甲数大
B.乙数大
C.一样大
D.无法比较
答案:2.
(2)B 【提示】由题意可知,$\frac {1}{甲数}>\frac {1}{乙数}$,因此甲数小于乙数。
(2)B 【提示】由题意可知,$\frac {1}{甲数}>\frac {1}{乙数}$,因此甲数小于乙数。
(3)已知a的$\frac{1}{4}$等于b的$\frac{1}{5}$(a、b 均不为0),则(
A.$a= b$
B.$a>b$
C.$b>a$
D.无法确定
C
)。A.$a= b$
B.$a>b$
C.$b>a$
D.无法确定
答案:2.
(3)C 【提示】假设$a×\frac {1}{4}=b×\frac {1}{5}=1$,则$a=4$,$b=5$,因此$b>a$。
(3)C 【提示】假设$a×\frac {1}{4}=b×\frac {1}{5}=1$,则$a=4$,$b=5$,因此$b>a$。
3. 两个自然数的倒数的和为$\frac{7}{12}$,这两个自然数分别是(
3
)和(4
)。答案:3.3 4 【提示】$\frac {1}{3}+\frac {1}{4}=\frac {7}{12}$,所以这两个自然数分别是3和4。
解析:
3和4
因为$\frac{1}{3} + \frac{1}{4} = \frac{4}{12} + \frac{3}{12} = \frac{7}{12}$,所以这两个自然数分别是3和4。
因为$\frac{1}{3} + \frac{1}{4} = \frac{4}{12} + \frac{3}{12} = \frac{7}{12}$,所以这两个自然数分别是3和4。
4. 已知$A×\frac{12}{11}= B×1= C×\frac{13}{11}= D×\frac{6}{7}$,并且A、B、C、D 都不为0,请把A、B、C、D 这四个数按照从大到小的顺序排列。
答案:4.$D>B>A>C$ 【提示】假设$A×\frac {12}{11}=B×1=C×\frac {13}{11}=D×\frac {6}{7}=1$,则$A=\frac {11}{12}$,$B=1$,$C=\frac {11}{13}$,$D=\frac {7}{6}$,因为$\frac {7}{6}>1>\frac {11}{12}>\frac {11}{13}$,所以$D>B>A>C$。
方法归纳
数量比较
此类型题可采用假设法,使题目具体化,先分别求出A、B、C、D的具体数量,再进行比较即可。
方法归纳
数量比较
此类型题可采用假设法,使题目具体化,先分别求出A、B、C、D的具体数量,再进行比较即可。
5. 甲数比乙数的倒数小1,乙数是丙数的倒数,丙数是3。甲数是多少?
答案:5.2 【提示】已知丙数是3,乙数是丙数的倒数,则乙数是$\frac {1}{3}$。又已知甲数比乙数的倒数小1,乙数的倒数是3,则甲数是$3-1=2$。
6. 比较$\frac{111}{1111}和\frac{1111}{11111}$的大小。
答案:6.$\frac {111}{1111}$的倒数是$\frac {1111}{111}$,$\frac {1111}{111}=10\frac {1}{111}$;$\frac {1111}{11111}$的倒数是$\frac {11111}{1111}$,$\frac {11111}{1111}=10\frac {1}{1111}$。因为$10\frac {1}{111}>10\frac {1}{1111}$,所以$\frac {111}{1111}<\frac {1111}{11111}$。
【提示】先求出两个分数的倒数,再通过比较倒数的大小来确定原分数的大小。一个分数的倒数越大,这个分数就越小;一个分数的倒数越小,这个分数就越大。
【提示】先求出两个分数的倒数,再通过比较倒数的大小来确定原分数的大小。一个分数的倒数越大,这个分数就越小;一个分数的倒数越小,这个分数就越大。
7. 新考法 规律探究 一张正方形纸,先由甲划去正方形面积的$\frac{1}{3}$,再由乙划去剩下面积的$\frac{1}{3}$,接着由甲划去剩下面积的$\frac{1}{3}$,再由乙划去剩下面积的$\frac{1}{3}$……这样一直划下去,想一想,第4次划去以后谁划去的面积大?如果这样不停地划下去,那么经过若干次后,谁划去的面积大呢?你能发现其中的规律吗?
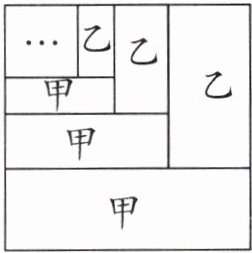

答案:7.第4次划去以后甲划去的面积大。经过若干次后,仍是甲划去的面积大。
【提示】假设正方形的面积为1,甲第一次划去$\frac {1}{3}$,乙第一次划去$(1-\frac {1}{3})×\frac {1}{3}=\frac {2}{9}$;甲第二次划去$(1-\frac {1}{3}-\frac {2}{9})×\frac {1}{3}=\frac {4}{27}$,乙第二次划去$(1-\frac {1}{3}-\frac {2}{9}-\frac {4}{27})×\frac {1}{3}=\frac {8}{81}$……对比前两次甲划去的面积和乙划去的面积,可见第4次后甲划去的面积大。如果这样不停地划下去,那么经过若干次后,甲划去的面积大,乙划去的面积始终是甲划去面积的$\frac {2}{3}$。
【提示】假设正方形的面积为1,甲第一次划去$\frac {1}{3}$,乙第一次划去$(1-\frac {1}{3})×\frac {1}{3}=\frac {2}{9}$;甲第二次划去$(1-\frac {1}{3}-\frac {2}{9})×\frac {1}{3}=\frac {4}{27}$,乙第二次划去$(1-\frac {1}{3}-\frac {2}{9}-\frac {4}{27})×\frac {1}{3}=\frac {8}{81}$……对比前两次甲划去的面积和乙划去的面积,可见第4次后甲划去的面积大。如果这样不停地划下去,那么经过若干次后,甲划去的面积大,乙划去的面积始终是甲划去面积的$\frac {2}{3}$。