(1)小敏吃了一块蛋糕的$\frac{1}{4}$,小华吃了剩下部分的$\frac{1}{3}$,小华吃了整块蛋糕的$\frac{
1
}{4
}$。答案:
(1)$\frac{1}{4}$ 【提示】小敏吃了一块蛋糕的$\frac{1}{4}$后,还剩这块蛋糕的$1-\frac{1}{4}=$$\frac{3}{4}$,小华吃了剩下的$\frac{1}{3}$,即小华吃了整块蛋糕的$\frac{3}{4}×\frac{1}{3}=\frac{1}{4}$。
(1)$\frac{1}{4}$ 【提示】小敏吃了一块蛋糕的$\frac{1}{4}$后,还剩这块蛋糕的$1-\frac{1}{4}=$$\frac{3}{4}$,小华吃了剩下的$\frac{1}{3}$,即小华吃了整块蛋糕的$\frac{3}{4}×\frac{1}{3}=\frac{1}{4}$。
解析:
小敏吃了蛋糕的$\frac{1}{4}$后,剩余蛋糕为$1 - \frac{1}{4} = \frac{3}{4}$。小华吃了剩下部分的$\frac{1}{3}$,即$\frac{3}{4} × \frac{1}{3} = \frac{1}{4}$。
$\frac{1}{4}$
$\frac{1}{4}$
(2)“冰融化成水后,体积减少了$\frac{1}{11}$”是把(
冰的体积
)看作单位“1”,(冰的体积
)×$\frac{1}{11}$= (冰融化成水后减小的体积
)。答案:
(2)冰的体积 冰的体积 冰融化成水后减小的体积
【提示】冰融化成水后,体积减少了$\frac{1}{11}$,即减少的体积是冰的体积的$\frac{1}{11}$。
(2)冰的体积 冰的体积 冰融化成水后减小的体积
【提示】冰融化成水后,体积减少了$\frac{1}{11}$,即减少的体积是冰的体积的$\frac{1}{11}$。
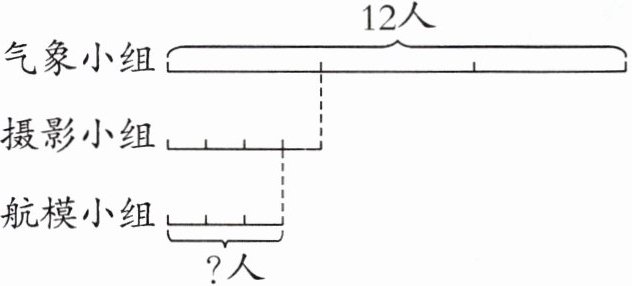
2. 看图列式计算。
]
]

答案:$12×\frac{1}{3}×\frac{3}{4}=3$(人) 【提示】气象小组有12人,摄影小组的人数是气象小组的$\frac{1}{3}$,摄影小组有$12×\frac{1}{3}=4$(人);航模小组的人数是摄影小组的$\frac{3}{4}$,航模小组有$4×\frac{3}{4}=3$(人)。
解析:
$12×\frac{1}{3}×\frac{3}{4}=3$(人)
(1)运送一些快递,甲车用了3小时,______,乙车用了多长时间?横线上填
A.甲车用的时间比乙车多$\frac{3}{5}$
B.乙车用的时间是甲车的$\frac{3}{5}$
C.甲车用的时间是乙车的$\frac{3}{5}$
D.乙车用的时间比甲车多$\frac{3}{5}$
B
,可用“$3×\frac{3}{5}$”求解。A.甲车用的时间比乙车多$\frac{3}{5}$
B.乙车用的时间是甲车的$\frac{3}{5}$
C.甲车用的时间是乙车的$\frac{3}{5}$
D.乙车用的时间比甲车多$\frac{3}{5}$
答案:
(1)B 【提示】根据题意,甲车用了3小时,求乙车用了多长时间,当列式为$3×\frac{3}{5}$时,说明乙车用的时间是甲车的$\frac{3}{5}$。
(1)B 【提示】根据题意,甲车用了3小时,求乙车用了多长时间,当列式为$3×\frac{3}{5}$时,说明乙车用的时间是甲车的$\frac{3}{5}$。
(2)x表示的数在图上的位置如图所示,则$\frac{1}{x}$表示的数大约会在(

A.a
B.b
C.c
D.d
C
)点上。
A.a
B.b
C.c
D.d
答案:
(2)C 【提示】观察数线可知,$\frac{1}{2}<x<1$,所以$1<$$\frac{1}{x}<2$。
(2)C 【提示】观察数线可知,$\frac{1}{2}<x<1$,所以$1<$$\frac{1}{x}<2$。
(3)如果x大于0,那么$x+\frac{1}{6}与x×\frac{1}{6}$相比较,(
A.$x+\frac{1}{6}$大
B.$x×\frac{1}{6}$大
C.一样大
D.无法确定哪个大
A
)。A.$x+\frac{1}{6}$大
B.$x×\frac{1}{6}$大
C.一样大
D.无法确定哪个大
答案:
(3)A 【提示】$x+\frac{1}{6}>x$,$x×\frac{1}{6}<x$,因此$x+$$\frac{1}{6}$大。
(3)A 【提示】$x+\frac{1}{6}>x$,$x×\frac{1}{6}<x$,因此$x+$$\frac{1}{6}$大。
4. 一辆汽车从甲地开往乙地,每小时行驶90千米,$\frac{4}{5}$小时刚好行驶到中点。甲、乙两地之间的距离是多少千米?
答案:$90×\frac{4}{5}×2=144$(千米)
【提示】根据题意可知,$\frac{4}{5}$小时行驶的路程正好是甲、乙两地之间距离的一半。
【提示】根据题意可知,$\frac{4}{5}$小时行驶的路程正好是甲、乙两地之间距离的一半。
5. 新考法 规律探究 先观察,再通过计算比较大小。
$\frac{4}{1×3}$
$\frac{8}{3×5}$
$\frac{12}{5×7}$
$\frac{16}{7×9}$
根据上面式子中蕴含的规律再写一道这样的式子:
计算:$\frac{4}{1×3}-\frac{8}{3×5}+\frac{12}{5×7}-\frac{16}{7×9}+\frac{20}{9×11}-\frac{24}{11×13}$
$\frac{4}{1×3}$
=
$\frac{1}{1}+\frac{1}{3}$$\frac{8}{3×5}$
=
$\frac{1}{3}+\frac{1}{5}$$\frac{12}{5×7}$
=
$\frac{1}{5}+\frac{1}{7}$$\frac{16}{7×9}$
=
$\frac{1}{7}+\frac{1}{9}$根据上面式子中蕴含的规律再写一道这样的式子:
$\frac{19}{8×11}=\frac{1}{8}+\frac{1}{11}$(等式不唯一)
。计算:$\frac{4}{1×3}-\frac{8}{3×5}+\frac{12}{5×7}-\frac{16}{7×9}+\frac{20}{9×11}-\frac{24}{11×13}$
$\frac{12}{13}$
答案:====$\frac{19}{8×11}=\frac{1}{8}+\frac{11}$(等式不唯一)
【提示】通过观察可以发现算式的特点:左边分数的分母是两个数相乘的积,分子是这两个数相加的和;右边是两个分数的和,两个分数的分子均是1,分母分别是左边分数分母中的两个数。符合这一特点的等式有无数道,如:$\frac{19}{8×11}=\frac{1}{8}+\frac{1}{11}$。
$\frac{4}{1×3}-\frac{8}{3×5}+\frac{12}{5×7}-\frac{16}{7×9}+\frac{20}{9×11}-\frac{24}{11×13}$
$=(\frac{1}{1}+\frac{1}{3})-(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})-(\frac{1}{7}+\frac{1}{9})+$$(\frac{1}{9}+\frac{1}{11})-(\frac{1}{11}+\frac{1}{13})$
$=\frac{1}{1}+\frac{1}{3}-\frac{1}{3}-\frac{1}{5}+\frac{1}{5}+\frac{1}{7}-\frac{1}{7}-\frac{1}{9}+\frac{1}{9}+\frac{1}{11}-$$\frac{1}{11}-\frac{1}{13}$
$=1-\frac{1}{13}$
$=\frac{12}{13}$
【提示】根据发现的规律,我们可以把算式中的每个分数看作两个分数的和,再通过去括号将一些分数互相抵消,从而使计算简便。
【提示】通过观察可以发现算式的特点:左边分数的分母是两个数相乘的积,分子是这两个数相加的和;右边是两个分数的和,两个分数的分子均是1,分母分别是左边分数分母中的两个数。符合这一特点的等式有无数道,如:$\frac{19}{8×11}=\frac{1}{8}+\frac{1}{11}$。
$\frac{4}{1×3}-\frac{8}{3×5}+\frac{12}{5×7}-\frac{16}{7×9}+\frac{20}{9×11}-\frac{24}{11×13}$
$=(\frac{1}{1}+\frac{1}{3})-(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})-(\frac{1}{7}+\frac{1}{9})+$$(\frac{1}{9}+\frac{1}{11})-(\frac{1}{11}+\frac{1}{13})$
$=\frac{1}{1}+\frac{1}{3}-\frac{1}{3}-\frac{1}{5}+\frac{1}{5}+\frac{1}{7}-\frac{1}{7}-\frac{1}{9}+\frac{1}{9}+\frac{1}{11}-$$\frac{1}{11}-\frac{1}{13}$
$=1-\frac{1}{13}$
$=\frac{12}{13}$
【提示】根据发现的规律,我们可以把算式中的每个分数看作两个分数的和,再通过去括号将一些分数互相抵消,从而使计算简便。