1. 某锅炉房要制作5根同样的长方体形状的通风管,管口是边长为4 dm的正方形,管长12 m。每平方米铁皮40元,制作这些通风管一共需要(
3840
)元铁皮。(接头处忽略不计)答案:3840 【提示】先求制作1根通风管需要铁皮的面积(通风管4个长方形面的面积之和),再求制作5根通风管需要铁皮的面积,然后根据“一共需要的钱数=每平方米铁皮的价钱×需要的铁皮总面积”求出答案。
解析:
4 dm = 0.4 m
1根通风管需要铁皮面积:0.4×12×4 = 19.2(m²)
5根通风管需要铁皮面积:19.2×5 = 96(m²)
一共需要的钱数:40×96 = 3840(元)
3840
1根通风管需要铁皮面积:0.4×12×4 = 19.2(m²)
5根通风管需要铁皮面积:19.2×5 = 96(m²)
一共需要的钱数:40×96 = 3840(元)
3840
2. 新考法 图形剪拼 有一张长30 cm、宽20 cm的长方形铁皮,从4个角上各剪去一个边长为5 cm的正方形,焊接成一个无盖的长方体铁盒(如下图)。这个铁盒的表面积是多少平方厘米?(接头处忽略不计)
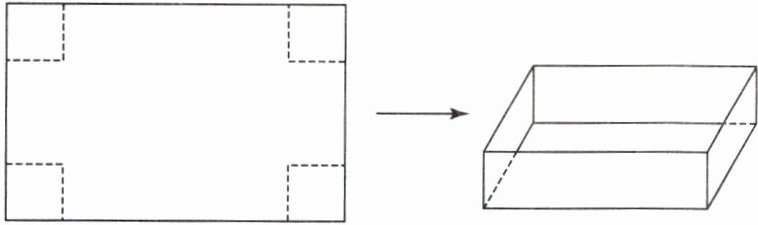

答案:30×20-5×5×4=500(cm²) 【提示】求这个铁盒的表面积,就是用长方形的面积减去剪掉的4个正方形的面积和。
解析:
$30×20 - 5×5×4 = 500\ \text{cm}^2$
(1)把一个表面积为150平方厘米的正方体的棱长扩大到原来的
A.8
B.4
C.2
C
倍,能够使正方体的表面积变为600平方厘米。A.8
B.4
C.2
答案:
(1)C 【提示】正方体的表面积扩大到原来的600÷150=4倍,则棱长扩大到原来的4÷2=2倍。
(1)C 【提示】正方体的表面积扩大到原来的600÷150=4倍,则棱长扩大到原来的4÷2=2倍。
(2)用两个相同的小长方体拼成一个大长方体,每个小长方体长15厘米,宽8厘米,高6厘米。拼成的大长方体的表面积最小是(
A.420
B.936
C.792
C
)平方厘米。A.420
B.936
C.792
答案:
(2)C 【提示】当长方体最大的面拼在一起时,拼成的大长方体的表面积最小。
(2)C 【提示】当长方体最大的面拼在一起时,拼成的大长方体的表面积最小。
4. 把一个正方体木块锯成两个大小不同的长方体,其中小长方体的表面积比大长方体的表面积少20平方厘米。原来正方体木块的棱长是5厘米,小长方体的表面积是多少平方厘米?
答案:(5×5×8-20)÷2=90(平方厘米) 【提示】把正方体木块锯成两个长方体后,增加了2个正方形的面,两个长方体的表面积之和相当于6+2=8(个)正方形的面积之和,即5×5×8=200(平方厘米)。小长方体的表面积比大长方体的表面积少20平方厘米,根据“和差问题”的求法可求出小长方体的表面积。
解析:
正方体一个面的面积:$5×5 = 25$(平方厘米)
两个长方体表面积之和:$6×25+2×25=8×25 = 200$(平方厘米)
小长方体表面积:$(200 - 20)÷2=90$(平方厘米)
答:小长方体的表面积是$90$平方厘米。
两个长方体表面积之和:$6×25+2×25=8×25 = 200$(平方厘米)
小长方体表面积:$(200 - 20)÷2=90$(平方厘米)
答:小长方体的表面积是$90$平方厘米。
5. 一个长方体的长为8厘米,上面与前面的面积之和为72平方厘米,右面的面积是上面的一半。求这个长方体的表面积。


答案:72÷8=9(厘米) 高:8÷2=4(厘米) 宽:9-4=5(厘米) (8×5+8×4+5×4)×2=184(平方厘米) 【提示】已知上面的面积+前面的面积=72厘米,则宽与高的和为72÷8=9(厘米)。又因为右面的面积是上面面积的一半,所以高就是长的一半,即高为8÷2=4(厘米)。
解析:
宽与高的和:$72÷8 = 9$(厘米)
高:$8÷2 = 4$(厘米)
宽:$9 - 4 = 5$(厘米)
表面积:$(8×5 + 8×4 + 5×4)×2$
$=(40 + 32 + 20)×2$
$=92×2 = 184$(平方厘米)
答:这个长方体的表面积是184平方厘米。
高:$8÷2 = 4$(厘米)
宽:$9 - 4 = 5$(厘米)
表面积:$(8×5 + 8×4 + 5×4)×2$
$=(40 + 32 + 20)×2$
$=92×2 = 184$(平方厘米)
答:这个长方体的表面积是184平方厘米。
6. 下面两个立体图形都是由棱长为1厘米的小正方体搭成的。

[我思考]立体图形①的表面积等于[(4+7+6)×2]个小正方形的面积之和,其中4、7、6分别是从上面、前面和右面观察到的小正方形的个数。
[我发现]根据立体图形①的表面积的求法,求立体图形②的表面积,列式为:
[我应用]如果添加同样的小正方体,把图②补充成一个长方体,那么这个长方体的表面积至少是多少平方厘米?

[我思考]立体图形①的表面积等于[(4+7+6)×2]个小正方形的面积之和,其中4、7、6分别是从上面、前面和右面观察到的小正方形的个数。
[我发现]根据立体图形①的表面积的求法,求立体图形②的表面积,列式为:
(9+7+7)×2=46(平方厘米)
[我应用]如果添加同样的小正方体,把图②补充成一个长方体,那么这个长方体的表面积至少是多少平方厘米?
(4×3+4×3+3×3)×2=66(平方厘米)
答案:(9+7+7)×2=46(平方厘米) (4×3+4×3+3×3)×2=66(平方厘米) 【提示】把图②补充成一个长方体,当这个长方体表面积最小时,长是4厘米,宽是3厘米,高是3厘米,根据长方体的表面积公式即可求出答案。
解析:
(9+7+7)×2=46(平方厘米)
(4×3+4×3+3×3)×2=66(平方厘米)
(4×3+4×3+3×3)×2=66(平方厘米)