1. 计算下面长方体和正方体的表面积。
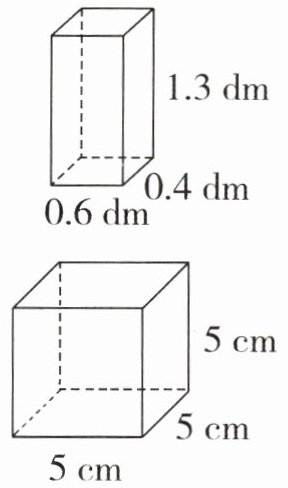

答案:(1.3×0.4+0.6×0.4+0.6×1.3)×2=3.08(dm²)
5×5×6=150(cm²)
【提示】长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的表面积=棱长×棱长×6。
5×5×6=150(cm²)
【提示】长方体的表面积=(长×宽+长×高+宽×高)×2,正方体的表面积=棱长×棱长×6。
2. 一个长方体的长是8厘米,宽和高都是5厘米,则这个长方体下面的面的面积是(
40
)平方厘米,表面积是(210
)平方厘米。答案:40 210 【提示】这个长方体下面的面是长8厘米、宽5厘米的长方形,有4个这样的面,左右是边长5厘米的正方形。
解析:
下面的面的面积:$8×5=40$平方厘米。
表面积:$2×(8×5 + 8×5 + 5×5)=2×(40 + 40 + 25)=2×105=210$平方厘米。
40 210
表面积:$2×(8×5 + 8×5 + 5×5)=2×(40 + 40 + 25)=2×105=210$平方厘米。
40 210
(1)李老师买了一块长方体形状的切糕,切糕长10厘米,宽8厘米,高5厘米。李老师按图中方式把它平均分成4块长方体形状的小切糕。一块小切糕的表面积是(

A.105
B.170
C.130
D.340
C
)平方厘米。
A.105
B.170
C.130
D.340
答案:
(1)C 【提示】一块小切糕的长是10÷2=5(厘米),宽是8÷2=4(厘米),高是5厘米,因此表面积是(5×4+5×5+5×4)×2=130(平方厘米)。
(1)C 【提示】一块小切糕的长是10÷2=5(厘米),宽是8÷2=4(厘米),高是5厘米,因此表面积是(5×4+5×5+5×4)×2=130(平方厘米)。
(2)新情境 手办盲盒 河南博物院推出的“仕女乐队”手办盲盒文创产品,该长方体育盒的底面是一个正方形。下面是这个长方体育盒的侧面展开图,这个长方体育盒的表面积是(

A.160
B.200
C.210
D.240
C
)平方厘米。
A.160
B.200
C.210
D.240
答案:
(2)C 【提示】长方体的底面边长是20÷4=5(厘米),长方体的表面积=20×8+5×5×2=210(平方厘米)。
(2)C 【提示】长方体的底面边长是20÷4=5(厘米),长方体的表面积=20×8+5×5×2=210(平方厘米)。
(3)实验班原创 应用意识 野战部队有一种长方体铁皮油箱,长和宽都是4 dm,高是5 dm,做80个这样的油箱至少需要
A.112
B.8960
C.9600
D.7680
8960
dm²铁皮。A.112
B.8960
C.9600
D.7680
答案:
(3)B 【提示】先求出1个油箱的表面积,再求出做80个这样的油箱至少需要多少平方分米铁皮。(4×5×4+4×4×2)×80=8960(dm²)。
(3)B 【提示】先求出1个油箱的表面积,再求出做80个这样的油箱至少需要多少平方分米铁皮。(4×5×4+4×4×2)×80=8960(dm²)。
4. 一个长方体,如果高增加4 cm,那么就变成一个正方体,这时表面积比原来增加$128 cm^2($如右下图)。原来长方体的表面

积
是多少平方厘米?
答案:128÷4÷4=8(cm) 8-4=4(cm)
8×4×4+8×8×2=256(cm²)
【提示】一个长方体,如果高增加4 cm,那么就变成一个正方体,说明这个长方体的底面是一个正方形,用“128÷4÷4”可求出底面的边长。
8×4×4+8×8×2=256(cm²)
【提示】一个长方体,如果高增加4 cm,那么就变成一个正方体,说明这个长方体的底面是一个正方形,用“128÷4÷4”可求出底面的边长。
5. 在棱长4分米的正方体的一个角上挖掉一个棱长1分米的小正方体(如右下图),所得立体图形的表面积是多少?


答案:4×4×6=96(平方分米)
【提示】在正方体的一个角上挖去一个小正方体,表面积不变。
【提示】在正方体的一个角上挖去一个小正方体,表面积不变。
6. 如右下图,把棱长8厘米的正方体木块锯成4个小长方体木块,表面积增加了多少平方厘米?


答案:8×8×4=256(平方厘米)
【提示】从图中可以看出,把正方体木块锯成4个小长方体木块,一共增加了4个正方形的面。
【提示】从图中可以看出,把正方体木块锯成4个小长方体木块,一共增加了4个正方形的面。