(1) 传统文化 蜡染 蜡染是我国民间传统纺织印染手工艺。制作5个蜡染抱枕和7块蜡染桌布需要650平方分米的布料,已知制作一个蜡染抱枕需要的布料是制作一块蜡染桌布的$\frac{1}{3}$,则制作一块蜡染桌布需要(
75
)平方分米的布料。答案:75 【提示】制作一个蜡染抱枕需要的布料是制作一块蜡染桌布的$\frac{1}{3}$,即制作一块蜡染桌布用的布料是制作一个蜡染抱枕的 3 倍。如果 650 平方分米的布料全部用来制作蜡染抱枕,那么可制作$5+7×3=26$(个),从而可求出制作一个蜡染抱枕所用的布料,进而求出制作一块蜡染桌布所用的布料。
解析:
设制作一块蜡染桌布需要$x$平方分米的布料,则制作一个蜡染抱枕需要$\frac{1}{3}x$平方分米的布料。
$5×\frac{1}{3}x + 7x = 650$
$\frac{5}{3}x + 7x = 650$
$\frac{5}{3}x + \frac{21}{3}x = 650$
$\frac{26}{3}x = 650$
$x = 650×\frac{3}{26}$
$x = 75$
75
$5×\frac{1}{3}x + 7x = 650$
$\frac{5}{3}x + 7x = 650$
$\frac{5}{3}x + \frac{21}{3}x = 650$
$\frac{26}{3}x = 650$
$x = 650×\frac{3}{26}$
$x = 75$
75
(2)5千克香蕉与3千克苹果的价钱相等,已知1千克苹果比1千克香蕉贵4元,则每千克香蕉(
6
)元。答案:6 【提示】根据题意可知,香蕉的单价$×5=$苹果的单价$×3$。设香蕉的单价为x元,则苹果的单价为$(x+4)$元。然后根据数量关系列方程即可解答。
解析:
设香蕉的单价为$x$元,则苹果的单价为$(x + 4)$元。
根据题意,$5x = 3(x + 4)$
$5x = 3x + 12$
$5x - 3x = 12$
$2x = 12$
$x = 6$
6
根据题意,$5x = 3(x + 4)$
$5x = 3x + 12$
$5x - 3x = 12$
$2x = 12$
$x = 6$
6
(3)已知$A+A+A+B+B+B+B= 100$,$A= 2B$,则$A=$
20
,$B=$10
。答案:20 10 【提示】由题意可知$3A+4B=100$,又$A=2B,3A=6B$,得$6B+4B=100$,解得$B=10$,$A=20$。
解析:
由题意得$3A + 4B = 100$,因为$A = 2B$,所以$3A = 3×2B = 6B$,则$6B + 4B = 100$,$10B = 100$,解得$B = 10$,$A = 2B = 2×10 = 20$。
$A = 20$,$B = 10$
$A = 20$,$B = 10$
2. 如下图,三种花分别有多少盆?
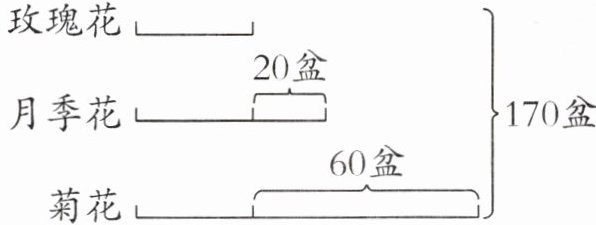

答案:玫瑰花:$(170-20-60)÷3=30$(盆)
月季花:$30+20=50$(盆)
菊花:$30+60=90$(盆)
【提示】如果月季花减少 20 盆,菊花减少 60 盆,那么三种花的盆数相等。因此用三种花的总盆数先减去$(20+60)$盆,再除以 3,即可求出玫瑰花的盆数,进而可求出月季花和菊花的盆数。
月季花:$30+20=50$(盆)
菊花:$30+60=90$(盆)
【提示】如果月季花减少 20 盆,菊花减少 60 盆,那么三种花的盆数相等。因此用三种花的总盆数先减去$(20+60)$盆,再除以 3,即可求出玫瑰花的盆数,进而可求出月季花和菊花的盆数。
(1)如图,前两架天平保持平衡,根据图中的等量关系,第三架天平右边放(
A.4
B.3
C.2
D.1
A
)个才能平衡。A.4
B.3
C.2
D.1
答案:A 【提示】由图可知,前两架天平都平衡,从第一架天平可以看出,1个大圆柱的质量等于1个小圆柱的质量加1个小正方体的质量。若在第二架天平左右两端各加上1个小正方体,结合第一架天平可知,1个小圆柱的质量等于2个小正方体的质量。第三架天平左边是2个小圆柱,2个小圆柱的质量等于4个小正方体的质量,因此右边放4个小正方体才能平衡。
(2)阿姨花160元买了一些水瓶和茶杯。每个水瓶25元,每个茶杯6元,买的茶杯比水瓶多6个。阿姨一共买了(
A.8
B.10
C.12
D.14
10
)个茶杯。A.8
B.10
C.12
D.14
答案:B 【提示】每个茶杯 6 元,6 个茶杯需要$6×6=36$(元),从 160 元中去掉这 36 元,则茶杯和水瓶的数量就一样多,因此阿姨一共买了$(160-36)÷(25+6)=4$(个)水瓶,买了$4+6=10$(个)茶杯。
4. 哥哥和弟弟一共收集了78枚邮票,哥哥给弟弟20枚后,哥哥和弟弟的邮票枚数同样多。哥哥和弟弟原来各有多少枚邮票?(先画线段图表示题中的数量关系,再解答)
答案:弟弟:$(78-20×2)÷2=19$(枚)
哥哥:$78-19=59$(枚)
【提示】由哥哥给弟弟 20 枚后,两人的邮票枚数同样多,可知原来哥哥比弟弟多$20×2=40$(枚)邮票,先求出弟弟的邮票枚数,再求出哥哥的邮票枚数。
易错警示
多多少的问题
哥哥给弟弟 20 枚后,哥哥和弟弟的邮票枚数同样多,说明哥哥比弟弟多$20×2=40$(枚)邮票,容易误认为哥哥比弟弟多 20 枚邮票。
哥哥:$78-19=59$(枚)
【提示】由哥哥给弟弟 20 枚后,两人的邮票枚数同样多,可知原来哥哥比弟弟多$20×2=40$(枚)邮票,先求出弟弟的邮票枚数,再求出哥哥的邮票枚数。
易错警示
多多少的问题
哥哥给弟弟 20 枚后,哥哥和弟弟的邮票枚数同样多,说明哥哥比弟弟多$20×2=40$(枚)邮票,容易误认为哥哥比弟弟多 20 枚邮票。
5. 甲、乙两地相距600千米,客车和货车同时从两地相对开出,经过4小时相遇。已知客车每小时比货车多行驶12千米,则客车每小时行驶多少千米?货车呢?
答案:客车:$(600÷4+12)÷2=81$(千米)
货车:$81-12=69$(千米)
【提示】客车和货车每小时共行驶$600÷4=150$(千米)。假设货车每小时多行驶 12 千米,则货车每小时行驶的路程与客车每小时行驶的路程相同,则客车每小时行驶$(150+12)÷2=81$(千米),货车每小时行驶$81-12=69$(千米)。
货车:$81-12=69$(千米)
【提示】客车和货车每小时共行驶$600÷4=150$(千米)。假设货车每小时多行驶 12 千米,则货车每小时行驶的路程与客车每小时行驶的路程相同,则客车每小时行驶$(150+12)÷2=81$(千米),货车每小时行驶$81-12=69$(千米)。
6. 新情境 国家补贴 为促进消费,2025年1月国家补贴政策出台。张大伯准备去商店买一台电冰箱,原价1500元,国家补贴后,在他付的钱里,只有面值50元和20元的人民币,其中20元的张数比50元的张数多10张,但20元的总钱数反而比50元的总钱数少250元。张大伯买这台电冰箱用了多少钱?
答案:$(250+20×10)÷(50-20)=15$(张)
$15+10=25$(张)
$50×15+20×25=1250$(元)
【提示】假设 20 元的张数减少 10 张,则 20 元的张数与 50 元的张数一样多,这时 20 元的总钱数比 50 元的总钱数少$250+20×10=450$(元),而 1 张 20 元比 1 张 50 元少$50-20=30$(元),从而可求出 50 元的张数为$450÷30=15$(张),20 元的张数为$15+10=25$(张),进而可求出张大伯买这台电冰箱一共用去的钱数。
$15+10=25$(张)
$50×15+20×25=1250$(元)
【提示】假设 20 元的张数减少 10 张,则 20 元的张数与 50 元的张数一样多,这时 20 元的总钱数比 50 元的总钱数少$250+20×10=450$(元),而 1 张 20 元比 1 张 50 元少$50-20=30$(元),从而可求出 50 元的张数为$450÷30=15$(张),20 元的张数为$15+10=25$(张),进而可求出张大伯买这台电冰箱一共用去的钱数。